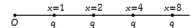A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Infinite charges of magnitude q each are lying at x= 1,2,4,8….meter on...
Text Solution
|
- Infinite charges of magnitude q each are lying at x= 1,2,4,8….meter on...
Text Solution
|
- An infinite number of charges, each of coulomb, are placed along x-axi...
Text Solution
|
- X - अक्ष पर x=1,2,4,8,... मीटर पर अनंत आवेश रखे गए हैं। इस आवेशों के क...
Text Solution
|
- An infinite number of charges each of magnitude q are placed on x-axis...
Text Solution
|
- X-अक्ष पर अनन्त आवेश, प्रत्येक q, क्रमशः x = 1, 2, 4, 8,.. मीटर पर रखे...
Text Solution
|
- An infinite number of charges, each of value q, are placed on the x-ax...
Text Solution
|
- Two point charges are placed on the y - axis at y = + a ...
Text Solution
|
- An ionfinite number of charges each q are placed in the x-axis at dist...
Text Solution
|