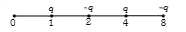A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- An infinite number of electric charges each equal to 5 nano-coulomb (m...
Text Solution
|
- An infinite number of electric charges each equal to 5 nano-coulomb (m...
Text Solution
|
- An infinite number of charges each numerically equal to q and of the...
Text Solution
|
- An infinite number of charges, each equal to Q=10 mu C are placed alon...
Text Solution
|
- An infinite number of charges, each of coulomb, are placed along x-axi...
Text Solution
|
- X-अक्ष पर अनन्त आवेश, प्रत्येक q, क्रमशः x = 1, 2, 4, 8,.. मीटर पर रखे...
Text Solution
|
- An infinite number of electric charges each equal to 5 nano coulombs a...
Text Solution
|
- An infinite number of electric charges each equal to 5 nano coulombs a...
Text Solution
|
- An infinite number of electric charges each equal to 5 nano coulombs a...
Text Solution
|