Home
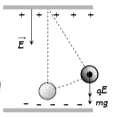
Class 12
PHYSICS
A small sphere carrying a charge q is ha...

A small sphere carrying a charge `q` is hanging in between two parallel plates by a string of length `L`. Time period of pendulum is `T_(0)`. When parallel plates are charged, the time period changes to `T`. The ratio `T//T_(0)` is equal to

A

`((g+(qE)/m)/g)^(1//2)`

B

`(g/(g+(qE)/m))^(3//2)`

C

`(g/(g+(qE)/m))^(1//2)`

D

None of these

Text Solution

Verified by Experts

The correct Answer is:
C
`T_0=2pisqrt(l//g)`
When `l rarr` constant then `T prop 1/sqrt(g.)`
`F_("net") implies mg. = mg +qE`
`implies g.= (g+(qE)/(m))`
`T=2pisqrt(l//g.)=2pisqrt(l/((g+(qE)/m))) `
Now `T/T_0=[(g)/(g+(qE)/m)]^(1//2)`
Promotional Banner

Similar Questions

Explore conceptually related problems

The time period of simple pendulum is T. If its length is increased by 2%, the new time period becomes

The temperatuire of a pendulum, the time period of which is t, is raised by DeltaT . The change in its time period is :

Time period of pendulum on earth surface is T_(1) . Its time period at a height equal to radius of earth is T_(2) , then the ratio of T_(1) : T_(2) is

A simple pendulum hanging from the ceiling of a stationary lift has a time period T 1 . When the lift moves downward with constant velocity, the time period is T, then

If the time period of a pendulum is 1sec , then what is the length of the pendulum at point of intersection of l-T and l-T^(2) graph.

For a simple pendulum, the graph between T^(2) and L (where T is the time period & Lis the length) is