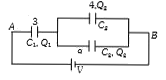
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- The combination of capacitors with C1 = 3muF , C2 = 4muF and C3 = 2mu ...
Text Solution
|
- IIf y=1+c1/(x-c1)+(c2x)/((x-c1)(x-c2))+(c3 x^2)/((x-c1)(x-c2)(x-c3)) s...
Text Solution
|
- what is the charge stored on each capacitor C1 and C2 in the circuit s...
Text Solution
|
- In the given circuit C1 = C, C2 = 2C, C3 = 3C. If charge at the capaci...
Text Solution
|
- C1, C2," और "C3, धारिता के तीन संधारित्र- (i) श्रेणीक्रम में और (ii) स...
Text Solution
|
- Two capacitors of capacitance C1" and "C2 are connected in parallel. I...
Text Solution
|
- C0 C1+C1 C2 + C2 C3+…+ C(n-1) Cn=
Text Solution
|
- दो संधारित्र जिनकी धारिताएँ C1 व् C2 है। यदि उन्हें समान आवेश दिए जाय...
Text Solution
|
- If C1, C2 , C3 , C4 are the coefficients of any consecutive terms in t...
Text Solution
|