A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
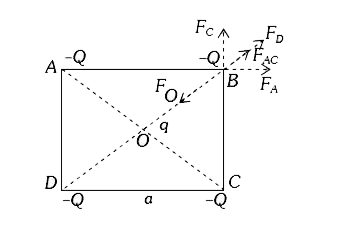
- Four charges equal to -Q are placed at the four corners of a square an...
Text Solution
|
- Four charges equal to -Q are placed at the four corners of a square an...
Text Solution
|
- Four charges equal to -Q are placed at the four corners of a square an...
Text Solution
|
- Four identical charges i.e. q is placed at the corners of a square of ...
Text Solution
|
- Four charges each of -Q, are placed at the four corners of a square. F...
Text Solution
|
- Four charges equal to Q are placed at the four comers of a square and ...
Text Solution
|
- Four identical charges each .q. are placed at four corners of a square...
Text Solution
|
- Four charges equal to - Q placed at the four corners of a sqare and a ...
Text Solution
|
- Four charges equal to - Q placed at the four corners of a sqare and a ...
Text Solution
|