Home
Class 12
PHYSICS
There is a uniform spherically symmetri...

There is a uniform spherically symmetric surface charge density at a distance `R_(0)` from the origin . The charge distribution is intially at rest and starts expanding because of mutual repulsion , the figure that repeesents best the speed V (r(t)) of the distribution as a function of its intantanradius R(t) is :

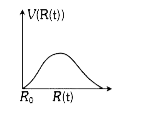
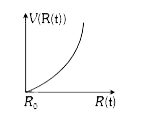
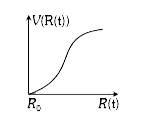
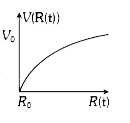
A

B

C

D

Text Solution

Verified by Experts

The correct Answer is:
D
`U_(i)+K_(i)=U_(f)+K_(f)`
`(KQ^(2))/(2r_(0))+0=(KQ^(2))/(2r)+(1)/(2)mv^(2)`
`v^(2)=(KQ^(2))/(m)((1)/(r_(0))-(1)/(r))`
`v=sqrt((KQ^(2))/(m)((1)/(r_(0))-(1)/(r)))`
Promotional Banner

Similar Questions

Explore conceptually related problems

There is a uniform spherically symmetric surface charge density at a distance R_(0) from the origin . The charge distribution is initially at rest and starts expanding because of mutual repulsion , the figure that represents best the speed V (r(t)) of the distribution as a function of its instant radius R(t) is :

For spherically symmetrical charge distribution, electric field at a distance r from the centre of sphere is vec(E)=kr^(7) vec(r) , where k is a constant. What will be the volume charge density at a distance r from the centre of sphere?

For a spherically symmetrical charge distribution electric field at a distance r from the centre of sphere is vec(E)=kr^(2)hat(r) where k is a constant what will be the volume charge density at a distance r from the centre of sphere?

The energy density u is plotted against the distance r from the centre of a spherical charge distribution on a log-log scale. Find the magnitude of slope of obtained straight line.

Consider a uniform charged sphere of charge density r and radius R.If the cavity of radius R/2is made inside the sphere and the removed part is again placed near the charge distribution as shown in the figure. If the electric field at the centre of the cavity is (rho R)/(n varepsilon_(0) find n .

A sphere of radius R_(0 carries a volume charge density proportional to the distance (x) from the origin, rho=alpha x where alpha is a positive constant.The total charge in the sphere of radius R_(0) is

A large plate with uniform surface charge density sigma is moving with constant speed v as shown in the figure. The magnetic field at a small distance from plate is

7.Consider a uniform charged sphere of charge density p and radius R.If the cavity of radius R/2is made inside the sphere and the removed part is again placed near the charge distribution as shown in the figure.If the electric field at the centre of the cavity is (rho R)/(n varepsilon_(0)) find n .

A uniformly charged disc of radius R having surface charge density sigma is placed in the xy plane with its center at the origin. Find the electric field intensity along the z-axis at a distance Z from origin :