A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
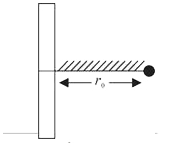
- A positive point charge is released from rest at a distance r 0 ...
Text Solution
|
- A charge particle q is released at a distance R(@) from the infinite l...
Text Solution
|
- The work done in bringing a unit positive charge from infinite distanc...
Text Solution
|
- किसी बिन्दु आवेश से दूरी r पर विद्युत् क्षेत्र अनुक्रमानुपाती होता है:
Text Solution
|
- A positive point charge is released from rest at a distance r 0 ...
Text Solution
|
- How is the potential at a distance 'r' from a point charge related to ...
Text Solution
|
- A positive charge released from rest
Text Solution
|
- विरामावस्था से एक बिन्दु धन आवेश को एक एकसमान घनत्व के धनात्मक रेखीय आ...
Text Solution
|
- A charge particle q is released at a distance R(@) from the infinite l...
Text Solution
|