A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
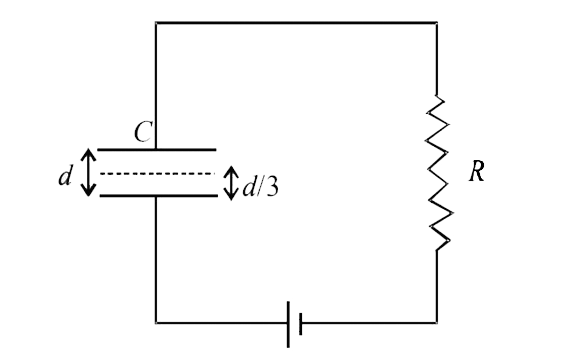
- A parallel plate capacitor C with plates of unit area and separation d...
Text Solution
|
- A parallel plate capacitor C with plates of unit area and separation d...
Text Solution
|
- Two conducting plates each having area A are kept at a separation d pa...
Text Solution
|
- Figure shows a horizontal parallel plate capacitor is lowered on a liq...
Text Solution
|
- The capacitance of a parallel plate air condenser is 10muF . When the ...
Text Solution
|
- Find an expression for the capacitance of a parallel plate capacitor w...
Text Solution
|
- एक समान्तर प्लेट संधारित्र C की प्लेटों का क्षेत्रफल इकाई तथा उनके बीच...
Text Solution
|
- P द्विध्रुव आघूर्ण के द्विध्रुव एक समान विद्युत क्षेत्र E में रखा है ...
Text Solution
|
- A parallel plate capacitor C with plates of area 1 square unit and sep...
Text Solution
|