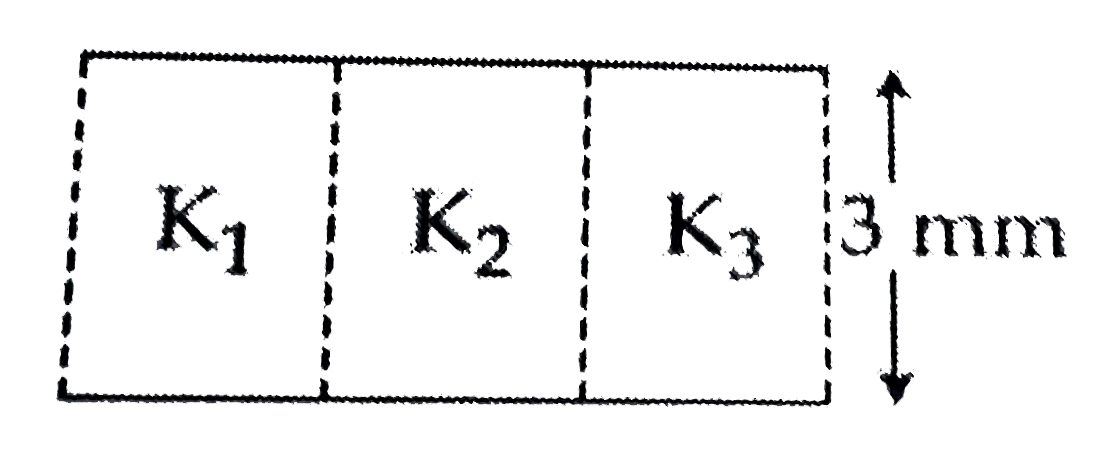A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A parallel plate capacitor is of area 6 cm^(2) and a separation 3 mm. ...
Text Solution
|
- Find the capacitance between A and B if two dielectric alabs (each of ...
Text Solution
|
- A parallel plate capacitor of area A , plate separation d and capacita...
Text Solution
|
- A parallel plate capacitor of area A, plate separation d and capacitan...
Text Solution
|
- A parallel plate capacitor with square plates is filed with four diele...
Text Solution
|
- A parallel plate capacitor is of area 6 cm^(2) and a separation 3 mm. ...
Text Solution
|
- The space between parallel plate capacitors is filled with four dielec...
Text Solution
|
- A parallel plate capacitor is of area 6cm^2 and a separation 4 mm. ...
Text Solution
|
- एक समान्तर प्लेट संधारित्र का क्षेत्रफल A, प्लेटो के मध्य दूरी d और धा...
Text Solution
|