A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
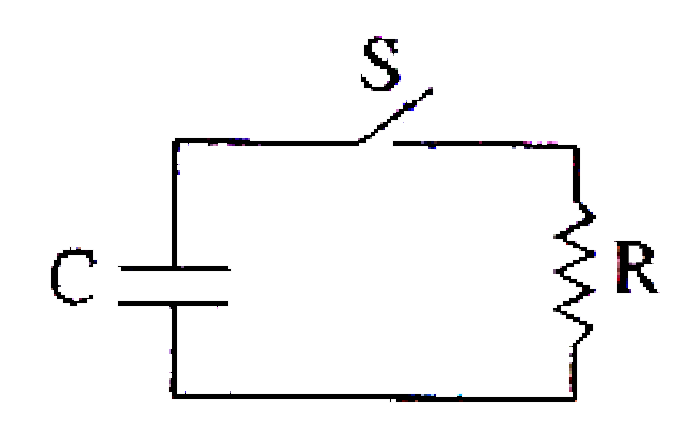
- The capacitor of capacitance C in the circuit shown in fully charged ...
Text Solution
|
- LetC be the capacitance of a capacitor discharging through a resistor ...
Text Solution
|
- In the circuit shown in fig. C1 = 2C2 Initially, capacitor C1 is charg...
Text Solution
|
- In the circuit shown, the capacitor C1 is initially charged with charg...
Text Solution
|
- At t=0 switch S is closed . Find (a) charge on capacitor after one t...
Text Solution
|
- The capacitor of capacitance C in the circuit shown in fully charged i...
Text Solution
|
- An L–C circuit contains inductor of inductance L and capacitor of capa...
Text Solution
|
- The capacitor shown in the figure is initially unchanged, the battery ...
Text Solution
|
- एक साधारण RC परिपथ को देखिए, जैसा चित्र 1 (Figure 1) में दर्शाया गया ह...
Text Solution
|