A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
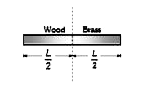
- A rod of length L is composed of a uniform length 1/2 L of wood mass i...
Text Solution
|
- Moment of inertia of a uniform rod of length L and mass M , about an a...
Text Solution
|
- Two uniform solid of masses m(1) and m(2) and radii r(1) and r(2) resp...
Text Solution
|
- The radius of gyration of an uniform rod of length L about an axis pas...
Text Solution
|
- A rod of length L is made of a uniform length L//2 of mass M(1) and a ...
Text Solution
|
- The moment of inertia of a thin uniform rod of mass M and length L abo...
Text Solution
|
- A rod of length L is composed of a uniform length 1/2 L of wood mass i...
Text Solution
|
- The moment of inertia of a thin uniform rod of mass M and length L abo...
Text Solution
|
- एक L लम्बाई की छड़ L/2 लम्बाई की लकड़ी की एकसमान छड़ ("द्रव्यमान "m(w)...
Text Solution
|