Home
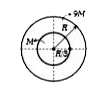
Class 11
PHYSICS
From a circular disc of radius R and ...

From a circular disc of radius R and 9M , a small disc of mass M and radius `(R )/(3)` is removed concentrically .The moment of inertia of the remaining disc about and axis perpendicular to the plane of the disc and passing through its centre is

A

`(40)/(9) MR^(2)`

B

`MR^(2)`

C

`4MR^(2)`

D

`(4)/(9) MR^(2)`

Text Solution

Verified by Experts

The correct Answer is:
A
`I= (9M (R)^(2))/(2)- (M ((R)/(3))^(2))/(2)`
`= (9MR^(2))/(2)- (MR^(2))/(18)= (80 MR^(2))/(18)`
`= (40MR^(2))/(9)`
Promotional Banner

Similar Questions

Explore conceptually related problems

Form a circular disc of radius R and mass 9M , a small disc of mass M and radius R/3 is removed concentrically . The moment of inertia of the remaining disc about an axis perpendicular to the the plane of the disc and passing its centre is :-

The moment of inertia of a uniform semicircular disc of mass M and radius r about a line perpendicular to the plane of the disc through the center is

The M.I. of a uniform semicircular disc of mass M and radius R about a line perpendicular to the plane of the disc and passing through the centre is

A thin disc of mass 9M and radius R from which a disc of radius R/3 is cut shown in figure. Then moment of inertia of the remaining disc about O, perpendicular to the plane of disc is -

A rectangular piece of dimension lxxb is cut out of central portion of a uniform circular disc of mass m and radius r. The moment of inertia of the remaining piece about an axis perpendicular to the plane of the disc and passing through its centre is :

The moment of inertia of a circular disc about an axis passing through the circumstances perpendicular to the plane of the disc is

Two thin discs each of mass M and radius r are attached as shown in figure, to from a rigid body. The rotational inertia of this body about an axis perpendicular to the plane of disc B and passing through its centre is : .