Home
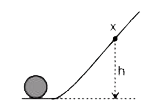
Class 11
PHYSICS
A solid sphere rolls without slipping, f...

A solid sphere rolls without slipping, first horizontal and then up to a point X at height h on an inclined plane before rolling down, as shown.

The initial horizontal speed of the sphere is

A

`sqrt((10gh)/(7))`

B

`sqrt((7gh)/(5))`

C

`sqrt((5gh)/(7))`

D

`sqrt(2gh)`

Text Solution

Verified by Experts

The correct Answer is:
A
`mgh = (1)/(2) mv^(2) + (1)/(2) (2)/(5) mR^(2) (v^(2))/(R^(2)) rArr mgh= (7)/(10) mv^(2)`
`rArr v= sqrt((10gh)/(7))`
Promotional Banner

Similar Questions

Explore conceptually related problems

Rolling (with and without slipping) on horizontal and inclined surface

A solid sphere rolls down without slipping from rest on a 30^@ incline. Its linear acceleration is

A 1 Kg solid sphere rolls without slipping on a rough horizontal suface as shown in figure. Select incorrect alternative

A solid sphere is rolling without slipping on a horizontal plane. The ratio of its rotational kinetic energy and translational kinetic energy is

A solid sphere rolls on a smooth horizontal surface at 10 m//s and then rolls up a smooth inclined plane of inclination 30^@ with horizontal. The mass of the sphere is 2 kg . Find the height attained by the sphere before it stops (in m ).

A solid sphere rolls down two different inclined planes of the same height but of different inclinations

A uniform solid sphere of radius R , rolling without sliding on a horizontal surface with an angular velocity omega_(0) , meets a rough inclined plane of inclination theta = 60^@ . The sphere starts pure rolling up the plane with an angular velocity omega Find the value of omega .

A solid sphere rolls without slipping down a 30^(@) inclined plane. If g=10 ms^(-2) then the acceleration of the rolling sphere is