A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
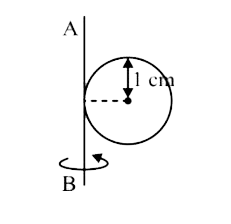
- A metal coin of mass 5 g and radius 1 cm is fixed to a think stick AB ...
Text Solution
|
- Find torque required so that a coin of mass 1kg rotates 25 revolution ...
Text Solution
|
- A mass m is attached to a rigid rod of negligible mass as shown in fig...
Text Solution
|
- A flywheel of mass 500 kg and diameter 1m is set in rotation. In 5 sec...
Text Solution
|
- Three massless rods are fixed to form a right angled triangular frame ...
Text Solution
|
- A mass of 10 kg connected at the end of a rod of negligible mass is ro...
Text Solution
|
- A solid cylinder of radius 0.5 m and mass 50 kg is rotating at 300 rpm...
Text Solution
|
- A metal coin of mass 5 g and radius 1 cm is fixed to a think stick AB ...
Text Solution
|
- 5g द्रव्यमान तथा 1cm त्रिज्या के धातु के एक सिक्के को एक पतली नगण्य द्...
Text Solution
|