Home
Class 11
PHYSICS
A small particle of mass m is projected...

A small particle of mass ` m` is projected at an angle `theta` with the ` x`- axis with an initial velocity ` v_(0)` in the ` x-y `plane as shown in the figure . At a time ` t lt ( v_(0) sin theta)/(g) `, the angular momentum of the particle is
where `hat (i) , hat (j) and hat(k)` are unit vectors along `x , y and z` - axis respectively.

A

`(1)/(2)mgv_(0)t^(2)cos thetahat(i)`

B

`-mgv_(0)t^(2)cos thetahat(j)`

C

`mgv_(0)tcos thetahat(k)`

D

`-(1)/(2)mgv_(0)t^(2)cos thetahat(k)`

Text Solution

Verified by Experts

The correct Answer is:
D
Angular momentum `vec(L)=vec(r)xxvec(p)`
Where, `vec(r)=v_(0)cos thetat hat(i)+(v_(0)sin thetat-(1)/(2)"gt"^(2))hat(j)`
`vec(p)=m[v_(0)costhetahat(i)+(v_(0)sintheta-"gt")hat(j)]`
`vec(L)=vec(r)xxvec(p)=-(1)/(2)mgv_(0)t^(2)costhetahat(k)`
Promotional Banner

Similar Questions

Explore conceptually related problems

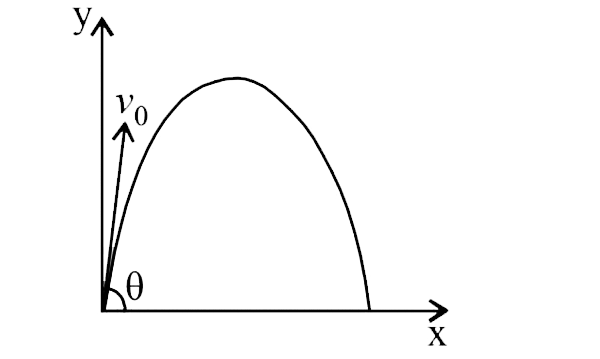
A small particle of mass m is projected at an angle theta with x-axis with initial velocity upsilon_(0) in x-y plane as shown in Fig. Calculate the momentum of the particle at t lt (upsilon_(0) sin theta)/(g) .

A small particle of mass m is projected at an angle theta with the x-axis, with initial velocity v_0 in the x-y plane. Just before time (2v_0sin theta) /g , the angular momentum of the particle about the point of projection is

The angle which the vector vec(A)=2hat(i)+3hat(j) makes with the y-axis, where hat(i) and hat(j) are unit vectors along x- and y-axis, respectively, is

A particle moves in x-y plane according to the equation bar(r ) = (hat(i) + 2 hat(j)) A cos omega t the motion of the particle is

Three particles , each of mass m, are placed at the vertices of a right angled triangle as shown in figure. The position vector of the center of mass of the system is (O is the origin and hat(i), hat(j), hat(k) are unit vectors)

A particle of mass m moves in the xy-plane with velocity of vec v = v_x hat i+ v_y hat j . When its position vector is vec r = x vec i + y vec j , the angular momentum of the particle about the origin is.