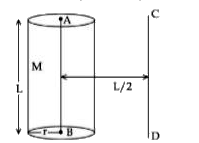
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- The solid cylinder of length 80 cm and mass M has a radius of 20 cm. C...
Text Solution
|
- Find the moment of inertia of a solid cylinder of mass M and radius R ...
Text Solution
|
- Calculate the moment of inertia of a cylinder of length 1.5 m , radius...
Text Solution
|
- What is moment of inertia of a solid cylinder of mass m, length l and ...
Text Solution
|
- The mass of the cylinder is 25 kg and radius of cylinder is 5 m. Find ...
Text Solution
|
- A solid cylinder of uniform density of radius 2 cm has mass of 50 g. ...
Text Solution
|
- एक ठोस बेलन की लम्बाई 1.5 मीटर, त्रिज्या 0.05 मीटर तथा घनत्व 8xx10^(3)...
Text Solution
|
- M द्रव्यमान और R त्रिज्या के एक ठोस बेलन का जड़त्व-आघूर्ण उसकी ज्यामित...
Text Solution
|
- Calculate the moment of inertia of a hollow cylinder of mass M and rad...
Text Solution
|