Home
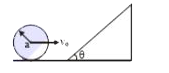
Class 11
PHYSICS
A sphere of radius 'a' and mass 'm' roll...

A sphere of radius 'a' and mass 'm' rolls along a horizontal plane with constant speed `v_(0)`. It encounters an inclined plane at angle `theta` and climbs upward. Assuming that it rolls without slipping, how far up the sphere will travel ?

A

`(2)/(5) (v_(0)^(2))/(gsintheta)`

B

`(v_(0)^(2))/(2g sin theta)`

C

`(v_(0)^(2))/(5g sin theta)`

D

`(7v_(0)^(2))/(10 g sin theta)`

Text Solution

Verified by Experts

The correct Answer is:
D

From energy conservation
`mgh=(1)/(2)mv_(0)^(2)+(1)/(2)Iomega^(2)`
`mgh=(1)/(2)mv_(0)^(2)+(1)/(2)xx(2)/(5)ma^(2)xx(v_(0)^(2))/(a^(2))`
`gh=(1)/(2)v_(0)^(2)+(1)/(5)v_(0)^(2)`
`gh=(7)/(10)v_(0)^(2)impliesh=(7v_(0)^(2))/(10g)`
From triangle `sintheta=(h)/(l)`
then `h=l sin theta`
`lsin theta=(7)/(10)(v_(0)^(2))/(g)`
`l=(7v_(0)^(2))/(10g sin theta)`
Promotional Banner

Similar Questions

Explore conceptually related problems

From an inclined plane a sphere, a disc, a ring and a shell are rolled without slipping. The order of their reaching at the base will be

A sphere of moment of inertia 'I' and mass 'm' rolls down on an inclined plane without slipping its K.E. of rolling is

A sphere of mass m and radius r rolls on a horizontal plane without slipping with a speed u . Now it rolls up vertically, then maximum height it would be attain will be

A sphere of mass 2 kg and radius 0.5 m is rolling with an initial speed of 1 ms^(-1) goes up an inclined plane which makes an angle of 30^(@) with the horizontal plane, without slipping, How long will the sphere take to return to the starting point A ?

A solid sphere of mass m and radius R rolls without slipping on a horizontal surface such that v_(c.m.)=v_(0) .

A uniform solid sphere rolls on a horizontal surface at 20 m/s. It, then, rolls up a plane inclined at

A drum of radius R and mass M, rolls down without slipping along an inclined plane of angle theta . The frictional force-