Home
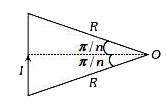
Class 12
PHYSICS
A loop carrying current I has the shape ...

A loop carrying current I has the shape of a regular polygon of n sides. If R is the distance from the centre to any vertex, then the magnitude of the magnetic induction vector `vec(B)` at the centre of the loop is –

A

`n"" (mu_(0) I)/(2pi R) "tan" (pi)/(n)`

B

`n"" (mu_(0) I)/(2pi R) "tan" (2pi)/(n)`

C

`(mu_(0) I)/(2R)`

D

`(mu_(0)I)/(pi R) "tan" (pi)/(n)`

Text Solution

Verified by Experts

The correct Answer is:
A
`B_(0) = (mu_(0))/(4pi ) (I)/(R cos"" (pi)/(n)) [ sin"" (pi)/(n) + sin "" (pi)/(n)]`
`B_(0) = (mu_(0))/(2pi) (I)/( R) "tan" (pi)/(n)`
`B = nB_(0) implies B = n ((mu_(0))/(2pi) (I)/( R) "tan" (pi)/(n))`
Promotional Banner

Similar Questions

Explore conceptually related problems

A wire bent in the shape of a regular n-polygonal loop carries a steady current I. Let l be the perpendicular distance of a given segment and R be the distance of vertex both from the centre of the loop. The magnitude of the magnetic field at the centre of the loop is given by -

In a regular polygon of n sides, each corner is at a distance r from the centre. Identical charges each of magnitude q are placed at corners. The field at the centre is

In a regular polygon of n sides, each corner is at a distance r from the centre. Identical charges of magnitude Q are placed at (n-1) corners. The field at the centre is

A circular loop of radius 9.7 cm carries a current 2.3 A. Obtain the magnitude of the magnetic field at the centre of the loop .

A current I flows through a thin wire shaped as regular polygon of n sides which can be inscribed in a circle of radius R. The magnetic fidl induction at the center of polygon due to one side of the polygon is

A square loop of side a carris a current I . The magnetic field at the centre of the loop is

The dipole moment of a circular loop carrying a current I, is m and the magnetic field at the centre of the loop is B_(1) . When the dipole moment is doubled by keeping the current constant, the magnetic field at the centre of the loop is B_(2) . The ratio (B_(1))/(B_(2)) is:

A square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is

A square loop is carrying a steady current I and the magnitude of its magnetic dipole moment is m. if this square loop is changed to a circular loop and it carries the current, the magnitude of the magnetic dipole moment of circular loop will be :