Home
Class 12
PHYSICS
A uniform but time-varying magnetic fiel...

A uniform but time-varying magnetic field B(t) exists in a circular region of radius a and is directed into the plane of the paper, as shown. The magnitude of the induced electric field at point P at a distance r from the centre of the circular region

A

Is zero

B

Decreases a `1/r`

C

Increases as r

D

Decreases as `1/r^2`

Text Solution

Verified by Experts

The correct Answer is:
B
`e=ointvecE.dvecl=|(dphi)/(dt)|=d/(dt)(BA cos 0^@)=A(dB)/(dt)`
`implies E xx2pir=pia^2(dB)/(dt)` for `r gt a`
`E = a^2/(2r) (dB)/(dt)implies E prop1/r`
Promotional Banner

Similar Questions

Explore conceptually related problems

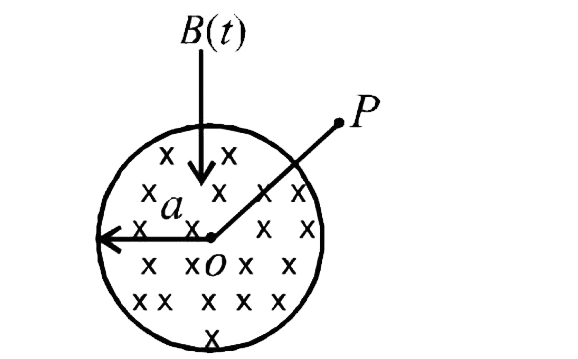
A uniform but time varying magnetic field B(t) exist in a circular region of radius a and is directed into the plane of the paper as shown. The magnitude of the induced electric field at point P at a distance r form the centre of the circular region.

A uniform magnetic field exists in a circular region of radius R centrad at O. The field is perpendicular to the plane of paper and is strength varies with time as B=B_(0)t . Find the induced electric field at a distance r from the centre for (i) r lt R , (ii) r gt R . Also, plot a graph between |E| and r for both the cases.

A uniform but time varying magnetic field is present in a circular region of radius R. The magnetic field is perpendicular and into the plane of the loop and the magnitude of field is increasing at a constant rate alpha . There is a straight conducting rod of length 2R placed as shown in figure. The magnitude of induced emf across the rod is

A uniform but time varying magnetic field B=(2t^3+24t)T is present in a cylindrical region of radius R =2.5 cm as shown in figure. The variation of electric field at any instant as a function of distance measured from the centre of cylinder in first problem is

The magnetic field in a certain cylindrical region is changing with time according to the law B=[16-4t^(2)] Tesla . The magnitude of induced electric field at point P at time t= time =2 sec , is