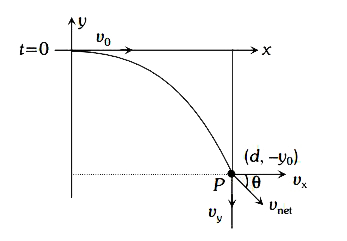
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A charged particle ( mass m and charge q) moves along X axis with velo...
Text Solution
|
- A positively charged particle, having charge q, is accelerated by a po...
Text Solution
|
- A particle of charge q and mass m moving with a velocity v along the x...
Text Solution
|
- A particle of mass m and charge q is thrown in a region where uniform ...
Text Solution
|
- A particle of mass m and charge Q moving with a velocity v enters a re...
Text Solution
|
- A uniform electric field of strength e exists in a region. An electron...
Text Solution
|
- A charge particle enters into a region containing uniform electric fie...
Text Solution
|
- A charge particle enters into a region containing uniform electric fie...
Text Solution
|
- A charged particle ( mass m and charge q) moves along X axis with velo...
Text Solution
|