Home
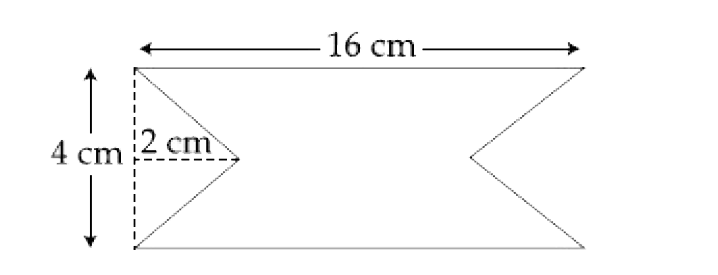
Class 12
PHYSICS
At time t=0 magnetic FIGUREield oFIGURE ...

At time t=0 magnetic FIGUREield oFIGURE 1000 Gauses is passing perpendicularly through the area deFIGUREined by the closed loop shown in the FIGUREigure. IFIGURE the magnetic FIGUREield reduces linearly to 500 Gauses, in the next 5s, then induces EMFIGURE in the loop is:

A

`28 muV`

B

`36 muv`

C

`48 muv`

D

`56 muv`

Text Solution

Verified by Experts

The correct Answer is:
D
`E=|-(dphi)/(dt)|=|-(AdB)/(dt)|`
`=(16xx4-4xx2)xx((1000-500))/5xx10^(-4)xx10^(-4)`
`=56 xx500/5 xx10^(-8)=56xx10^(-6)V=56muV`
Promotional Banner

Similar Questions

Explore conceptually related problems

Assertion A conducting loop is rotated in a uniform magnetic field with constant angular velocity omega as shown in figure. At time t = 0, plane of the loop is perpendicular to the magnetic field. Induced emf produced in the loop is maximum when plane of loop is parallel to magnetic field. Reason When plane of loop is parallel to magnetic field, then magnetic flux passing through the loop is zero.

A wire bent as a parabola y=kx^(2) is located in a uniform magnetic field of induction B, the vector B being perpendicular to the plane xy. At t=0 , the sliding wire starts sliding from the vertex O with a constant acceleration a linearly as shown in Fig. Find the emf induced in the loop -

A square loop of side 20 cm and resistance 0.30 Omega is placed in a magnetic field of 0.4 T. The magnetic field is at an angle of 45^(@) to the plane of loop. If the magnetic field is reduced to zero in 0.5 s, then find the induced emf and induced current in the loop in this time interval.

The magnetic field through a circular loop of wire 12 cm in radius and 8.5 ohm resistance, changes with time as shown in Fig. The magnetic field is perpendicular to the plane of the loop. Calculate the induced current in the loop and plot is as a function of time.

A uniform magnetic field B exist in a direction perpedicuar to the plane of a square loop made of a metal wire. The wire has diameter of 4 mm and a total length of 30 cm . The magnetic field changes with time at a steady rate dB/dt = 0.032 T s^(-1) . The induced current in the loop is close to (Resistivity of the metal wire is 1.23 xx 10^(-8) Omega m )

The magnetic field perpendicular to the plane of a loop of area 0.5 m^2 is 0.6 T . Calculate the magnetic flux through the loop (in weber)

A conducting circular loop is placed in a magnetic field of strength 0.04 T, such that the plane of the loop is perpendicular to the magnetic field. If the radius of the loop begins to shrink at a constant rate of 0.5 mm // s , then calculate the emf induced in the loop when its radius is 1.5 cm.

The figure shows a uniform, 3.0 T magnetic field that is normal to the plane of a conducting, circular loop with a resistance of 1.5 Omega and a radius of 0.024 m. The magnetic field is directed out of the paper as shown . Note: The area of the non-circular portion of the wire is considered negligible compared to that of the circular loop. If the magnetic field is held constant at 3.0 T and the loop is pulled out of the region that contains the field in 0.2 s, what is the magnitude of the average induced emf in the loop?

A loop of flexible conducting wire of length 0.5 m lies in a magnetic field of 1.0 T perpendicular to the plane of the loop. Show that when a current as shown in Fig. 1.112 is passed through the loop, it opens into a circle. Also calculate the tension developed in the wire if the current is 1.57 A.

A square conductind loop, 20.0 cm on a side placed in the same magnetic field as shown in Fig. 3.195, center of the magnetic field region, where dB//dt = 0.035 T s^(-1) . The current induced in the loop if its resistance is 2.00 Omega is