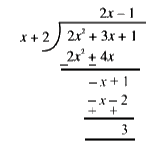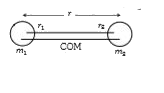A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A diatomic molecule is made of two masses m(1) and m(2) which are sepa...
Text Solution
|
- The key feature of Bohr'[s spectrum of hydrogen atom is the quantizati...
Text Solution
|
- A diatomic molecule is madde of two masses m(1) and m(2) which are sep...
Text Solution
|
- एक द्विपरमाण्विक अणु में दुरी r पर द्रव्यमान m(1) व m(2) के दो परमाणु ...
Text Solution
|
- A diatomic molecule is made of two masses m(1)andm(2) which are separa...
Text Solution
|
- A diatomic molecules is made of two masses m(2) and m(2) which are sep...
Text Solution
|
- एक द्विपरमाणुक अणु m(1) तथा m(2) के दो द्रव्यमानो से बना है जोको दूरी...
Text Solution
|
- एक द्विपरमाणुक अणु m(1) तथा m(2) के दो द्रव्यमानों से बना है जो कि दूर...
Text Solution
|
- A diatomic molecule is made of two masses m(1) and m(2) which are sepa...
Text Solution
|