Home
Class 12
PHYSICS
At time t = 0, a material is composed of...

At time t = 0, a material is composed of two radioactive atoms A and B, where `N_(A0) = 2N_(B0)`.
The decay constant of both kind of radioactive atoms is `lamda` . However, A disintegrates to B and B disintegrates to C. Which of the following figures represents the evolution of `N_B(t)//N_B(0)` with respect to time t?
[`N_A(0)=`No. of A atoms at t = 0]
[`N_B(0)=` No. of B atoms at t= 0 ]

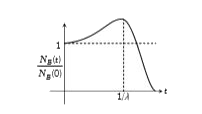
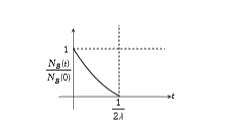
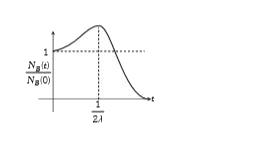
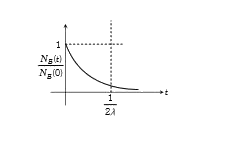
A

B

C

D

Text Solution

Verified by Experts

The correct Answer is:
C
`A to B , B to C `
`(dN_(B))/(dt) = lambdaN_(A) - lambdaN_(B)`
`(dN_(B))/(dt) =2lambdaN_(B_(0))e^(-lambdat) -lambdaN_(B)`
`e^(-lambdat)((dN_(B))/dt+lambdaN_(B))=2lambdaNB_(0)e^(-lambdat) xx e^(lambdat)`
`d/(dt)(N_(B)e^(lambdat))=2lambdaN_(B_(0)) ` , on integrating
` N_(B)e^(lambdat) = 2lambdatN_(B_(0))+N_(B_(0))`
`N_(B) = N_(B_(0))[1 +2 lambdat]e^(-lambdat)`
`(dN_(B))/dt = 0 " at " -lambda t [1 + 2 lambdat )e^(-lambdat) +2lambdae^(-lambdat) = 0 `
`N_(B_(max)) " at " t = 1/(2lambda)` .
Promotional Banner

Similar Questions

Explore conceptually related problems

The radioactive sources A and B of half lives of t hr and 2t hr respectively, initially contain the same number of radioactive atoms. At the end of t hours, their rates of disintegration are in the ratio:

The graph between number of decayed atoms N' of a radioactive element and time t is.

At time t = 0, a container has N_(0) radioactive atoms with a decay constant lambda . In addition, c numbers of atoms of the same type are being added to the container per unit time. How many atoms of this type are there at t = T ?

A stable nuclei C is formed from two radioactive nuclei A and B with decay constant of lambda_1 and lambda_2 respectively. Initially, the number of nuclei of A is N_0 and that of B is zero. Nuclei B are produced at a constant rate of P. Find the number of the nuclei of C after time t.

Two radioactive materials A & B have decay constant 3lamda and 2lamda respectively. At t=0 the numbers of nuclei of A and B are 4N_(0) and 2N_(0) respectively then,

The number of atoms of a radioactive substance of half-life T is N_(0) at t = 0. The time necessary to decay from N_(0)//2 atoms to N_(0)//10 atoms will be

A sample of a radioactive nucleus A disintegrates to another radioactive nucleus B, which in turn disintegrates to some other stable nucleus C. Plot of a graph showing the variation of number of atoms of nucleus B vesus time is : (Assume that at t = 0, there are no B atoms in the sample)