A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
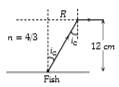
- A fish looking up through the water sees the outside world contained i...
Text Solution
|
- A fish looking up through the water sees the outside world contained i...
Text Solution
|
- A fish looking up through the water sees the outside world contained i...
Text Solution
|
- A fist looking from within water sees the outside world through a circ...
Text Solution
|
- A fish at a depth of sqrt(7) cm bleow the surface of water sees the ou...
Text Solution
|
- पानी के भीतर कोई मछली ऊपर की ओर बाहरी दुनिया को वृत्तीय क्षितिज में स...
Text Solution
|
- A fish looking up through the water see the outside world, contained i...
Text Solution
|
- एक मछली पानी में ऊपर की ओर वृताकार क्षैतिज में बाह्य दुनिया को देखती ह...
Text Solution
|
- A fish looking up through the water sees the outside world contained i...
Text Solution
|