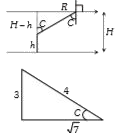
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- On a bright sunny day a diver of height h stands at the bottom of a la...
Text Solution
|
- When a large bubble rises from the bottom of a lake to the surface its...
Text Solution
|
- On a bright sunny day a diver of height h stands at the bottom of a la...
Text Solution
|
- A fish situated at a depth h below the surface of water in a lake ,can...
Text Solution
|
- If we see the outside objects by keeping an eye at a depth h inside wa...
Text Solution
|
- A air bubble rises from bottom of a lake to surface. If its radius inc...
Text Solution
|
- A point source of light is placed at the bottom of a water lake. If th...
Text Solution
|
- rho ঘনত্ববিশিষ্ট একটি বস্তুকে rho'(rho'ltrho) ঘনত্ববিশিষ্ট হ্রদের জলে...
Text Solution
|
- An air bubble doubles in radius on rising from the bottom of a lake to...
Text Solution
|