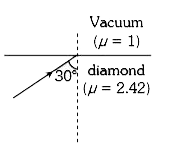
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A ray of laser of a wavelength 630 nm is incident at an angle of 30^(@...
Text Solution
|
- The refractive index of air with respect to glass is 2//3. The refract...
Text Solution
|
- If the refractive index for light going from air to diamond be 2.42, w...
Text Solution
|
- एक प्रकाश किरण वायु से हीरे में प्रवेश करती है प्रकाश की चाल में कितने...
Text Solution
|
- The diamond has refractive index of 2.4 for sodium light of wavelength...
Text Solution
|
- Refractive index of glass is 1.5 and of diamond is 2.42. Calculate the...
Text Solution
|
- The refractive index of air with respect to glass is 2//3 . The refrac...
Text Solution
|
- वायु के सापेक्ष काँच का अपवर्तनांक 1.50 है तथा काँच के सापेक्ष हीरे का...
Text Solution
|
- The speed of light in air is 3xx10^8 m/s. Find its speed in diamond if...
Text Solution
|