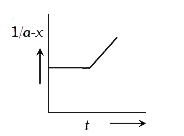
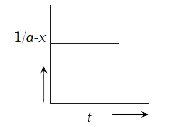
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- For the reaction A to Product k=(1)/(t)[(1)/(a-x)-(1)/(a)] Where ...
Text Solution
|
- Following is the graph between (a-x) and time t for second order react...
Text Solution
|
- Graph between log k and 1//T [k rate constant (s^(-1)) and T and the t...
Text Solution
|
- For a reation: A rarr Product, rate law is -(d[A])/(dt)=K[A](0) . The ...
Text Solution
|
- Surface catalysed reaction that are inhibited by the products obey the...
Text Solution
|
- Graph between log k and (1)/(T) (k is rate constant in s^(-1) and T is...
Text Solution
|
- Graph between log k and 1//T [where K is rate constant in s^(-1) and T...
Text Solution
|
- Match order of the reaction (in List-I) with the corresponding rate co...
Text Solution
|
- The graph between log k and 1/T[K is rate constant (sec^(-1)) and T th...
Text Solution
|