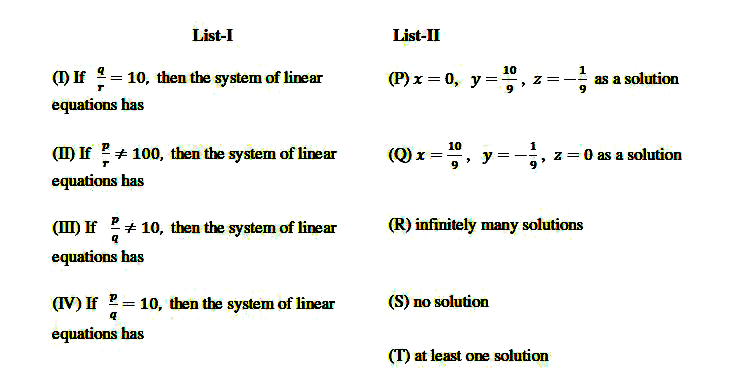A
B
C
D
Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
JEE ADVANCED PREVIOUS YEAR-JEE ADVANCED 2022-MATHEMATICS (SECTION -3)
- Consider the following lists : The correct option is :
Text Solution
|
- Two players P(1) and P(2) play a game against each other . In every ro...
Text Solution
|
- Let p , q , r be nonzero real numbers that are respectively , the 10^(...
Text Solution
|
- Consider the ellipse (x^(2))/(4) + (y^(2))/(3) = 1 Let H(alpha , 0...
Text Solution
|