A
B
C
D
Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
CBSE MODEL PAPER-SAMPLE PAPER 2023 TERM I-SECTION E
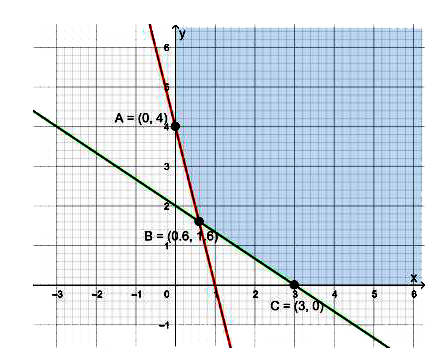
- The corner points of the shaded unbounded feasible region of an LPP ar...
Text Solution
|
- Read the following passage and answer the questions given below. ...
Text Solution
|
- Read the following passage and answer the questions given below. ...
Text Solution
|
- Read the following passage and answer the questions given below. ...
Text Solution
|
- Read the following passage and answer the questions given below. ...
Text Solution
|
- Read the following passage and answer the questions given below. ...
Text Solution
|
- Read the following passage and answer the questions given below. ...
Text Solution
|
- Read the following passage and answer the questions given below. ...
Text Solution
|
- Read the following passage and answer the questions given below. ...
Text Solution
|
- Read the following passage and answer the questions given below. ...
Text Solution
|
- Read the following passage and answer the questions given below. ...
Text Solution
|