Topper's Solved these Questions
SAMPLE PAPER 2023 TERM I
CBSE MODEL PAPER|Exercise Section E|12 VideosSAMPLE PAPER 2023 TERM I
CBSE MODEL PAPER|Exercise SECTION-A|20 VideosSAMPLE PAPER 2023 TERM I
CBSE MODEL PAPER|Exercise Section C|8 VideosSAMPLE PAPER 2022 TERM II
CBSE MODEL PAPER|Exercise SECTION C|10 VideosSAMPLE PAPER 2024
CBSE MODEL PAPER|Exercise Question|94 Videos
Similar Questions
Explore conceptually related problems
CBSE MODEL PAPER-SAMPLE PAPER 2023 TERM I-Section D
- An express train takes 1 hour less than a passenger train to travel...
Text Solution
|
- A motor boat whose speed is 18 km/h m still water takes 1 hour more...
Text Solution
|
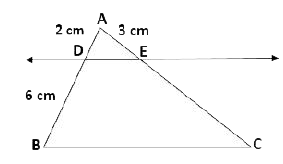
- Prove that If a line is drawn parallel to one side of a triangle to in...
Text Solution
|
- A pen stand made of wood is in the shape of a cuboid with four conical...
Text Solution
|
- Ramesh made a bird-bath for his garden in the shape of a cylinder with...
Text Solution
|
- A life insurance agent found the following data for distribution of ag...
Text Solution
|