Similar Questions
Explore conceptually related problems
Recommended Questions
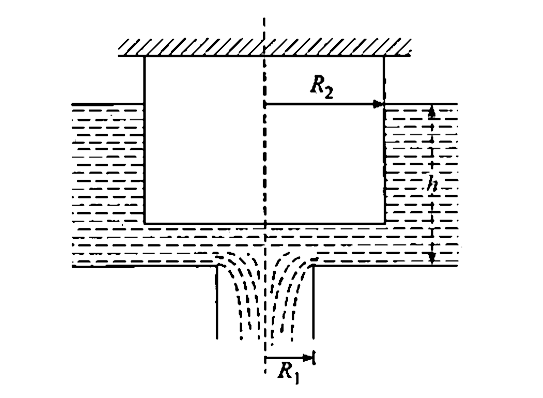
- The horizontal bottom of a wide vessel with an ideal fluid has a round...
Text Solution
|
- A U-tube rotates with angular velocity omega about the vertical axis A...
Text Solution
|
- The horizontal bottom of wide vessel with an ideal fluid has a round o...
Text Solution
|
- The horizontal bottom of a wide vessel with an ideal fluid has a round...
Text Solution
|
- If a vessel containing a fluid of density rho upto height h is acceler...
Text Solution
|
- साबुन के दो बुलबले जिनके त्रिज्याएँ r(1) व r(2)(r(1)gt r(2)) है , मि...
Text Solution
|
- एक बर्तन की तली क्षेत्रफल A तथा इसमें भरे द्रव का घनत्व d एवं ऊंचाई h ...
Text Solution
|
- द्रव से भरे पात्र की तली पर दाब निर्भर नहीं करता है-
Text Solution
|
- (i) वायु में द्रव के बुलबुले , (ii) द्रव में वायु के बुलबुले की त्रिज्...
Text Solution
|