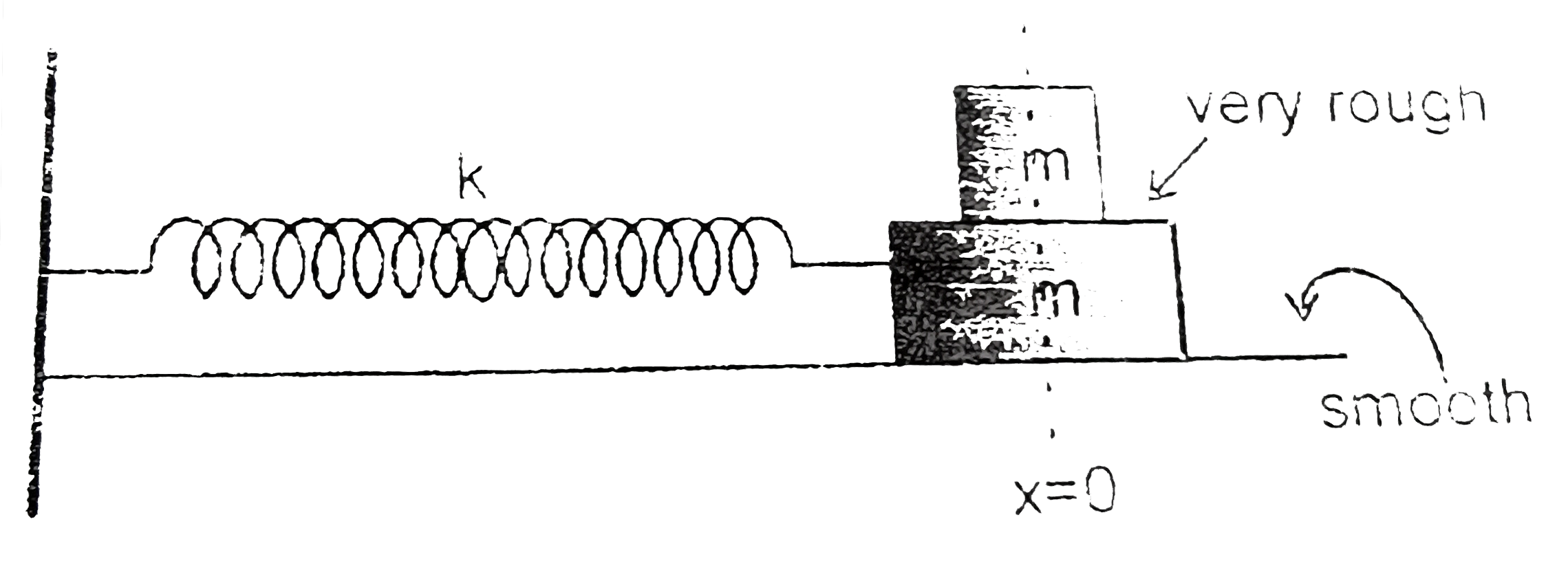Similar Questions
Explore conceptually related problems
Recommended Questions
- The given system is displacement by distance 'A' and released. Both th...
Text Solution
|
- A block P of mass m is placed on horizontal frictionless plane. A seco...
Text Solution
|
- The coefficient of friction between block of mass m and 2m is mu=2tant...
Text Solution
|
- When distance between two given magnetic poles is halved, force betwee...
Text Solution
|
- The coefficient of friction between the block A of mass m & block B of...
Text Solution
|
- The given system is displacement by distance 'A' and released. Both th...
Text Solution
|
- The coefficient of friction between the block A of mass m & block B of...
Text Solution
|
- A block of mass m is kept on an inclined plane of mass 2m and inclinat...
Text Solution
|
- A block Q of mass 2m is placed on a horizontal frictionless plane. A s...
Text Solution
|