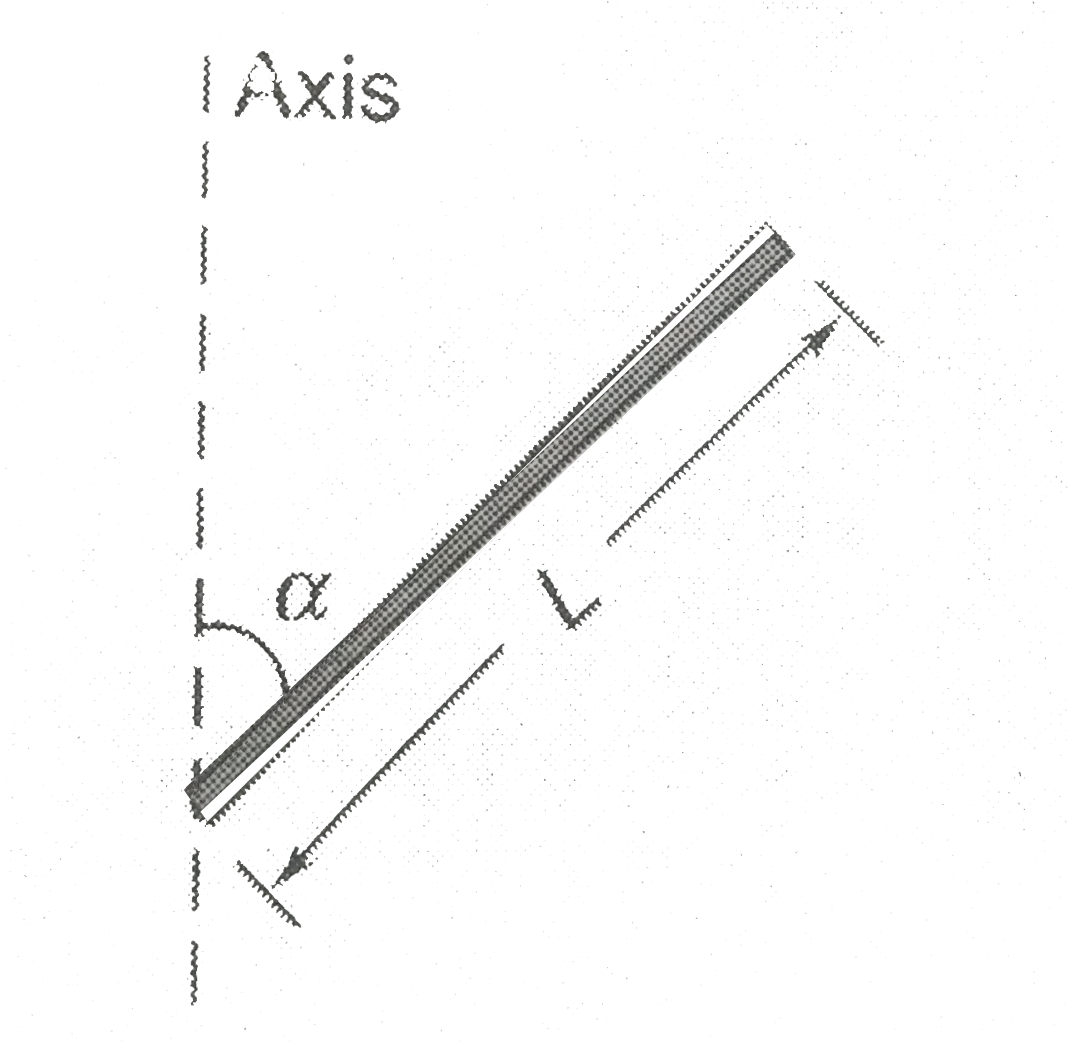Similar Questions
Explore conceptually related problems
Recommended Questions
- Find the M.I. of thin uniform rod of mass M and length L about the axi...
Text Solution
|
- Find the moment of inertia of the rod AB about an axis yy as shown in ...
Text Solution
|
- Three thin, uniform, indentical rods each or mass M and length L are j...
Text Solution
|
- Two thin uniform rods A ( M.L ) and B ( 3M,3L ) are joined as shown. F...
Text Solution
|
- Find the M.I. of thin uniform rod of mass M and length L about the axi...
Text Solution
|
- The moment of inertia of a thin uniform rod of mass M and length L abo...
Text Solution
|
- Calculate the moment of inertia of a thin rod of mass m and length l a...
Text Solution
|
- The moment of inertia of a thing uniform rod of length L and mass M , ...
Text Solution
|
- The M.I. of thin uniform rod of mass 'M' and length 'l' about an axis ...
Text Solution
|