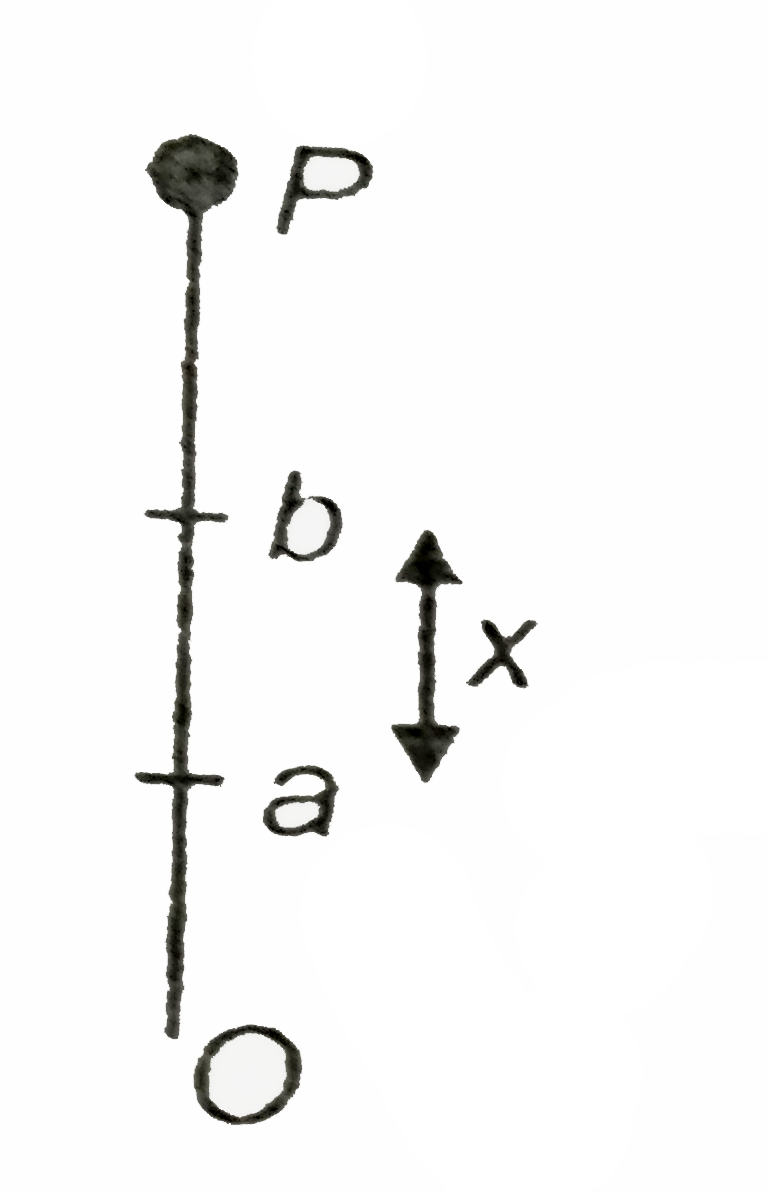Home
Class 12
PHYSICS
An object is thrown vertically upward wi...

An object is thrown vertically upward with some speed. It crosses ` 2` points ` p,q` whith are separated by (h) metre. If (t) is the time between (p) and highest point and coming back and ` t_(q)` is the time between `q` and highest point and coming back, relate acceleration due to gravity `t_(p),t_(q) and h`.

Text Solution

Verified by Experts

Strategy: Let u' be velocity of the object while crossing point a and v' be its velocity while crossing point b. As shown P is the highest point of vertical motion of object. The time taken by the object in going a to `P=t_(a//2)` the time taken by the object in going from b to `P=(t_(0))/(2)`

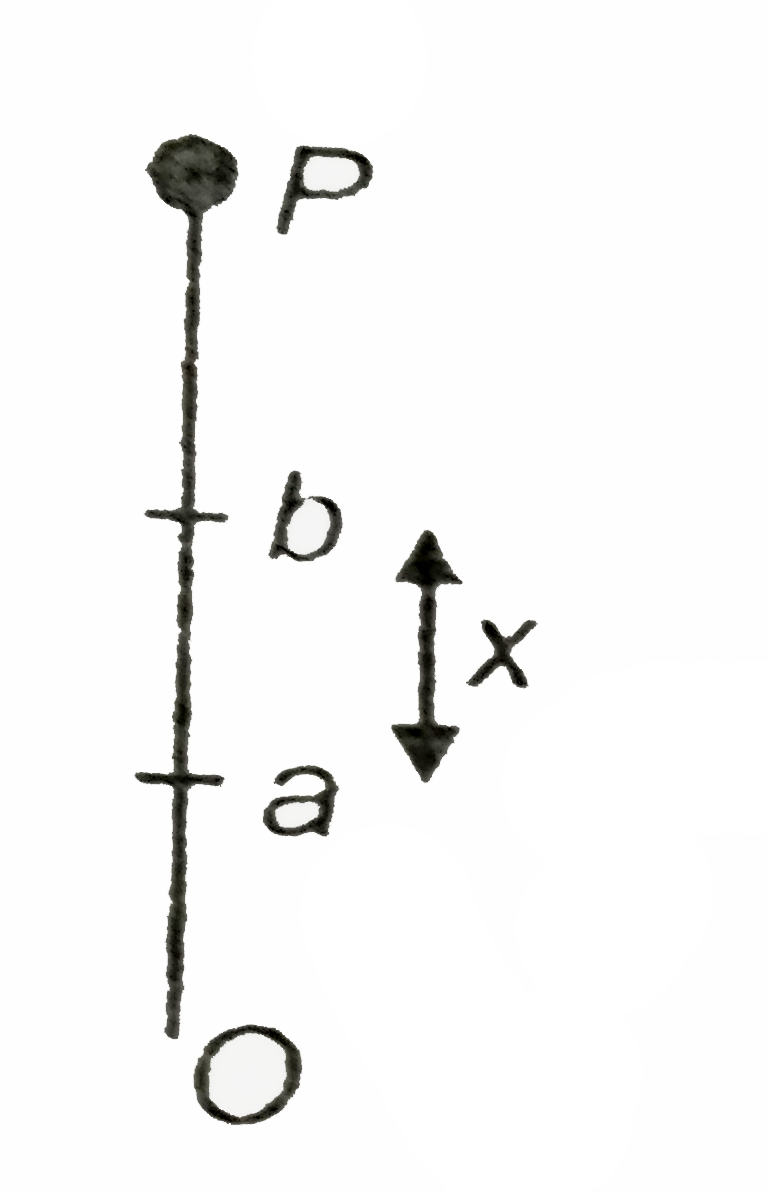
Taking vertical upward motion of object from a to P we have
`u=v', v=0, a = -g, t=(t_(a))/(2)`
As, `v=u+at`
`therefore" "0=u'+(-g)(t_(a))/(2)" or "u'=(g t_(a))/(2)" ...(i)"`
Taking vertical upward motion of object from b to P, we have
`u=v', v=0, a=-g, t=(t_(b))/(2)`
As, `v=u+at`
`0=v'(-g)(t_(b))/(2)" or "v'=(g t_(b))/(2)" ...(ii)"`
Taking vertical upward motion of object from a to b, we have
`u=u', v=v',a=-g,s=x`
As, `v^(2)=u^(2)+2as`
`therefore" "v'^(2)=u'^(2)+2(-g)(x)`
`"or "2gx=u'^(2)-v'^(2)=(g^(2)t_(a)^(2))/(4)-(g^(2)t_(b)^(2))/(4)`
`2gx=(g^(2))/(4)[t_(a)^(2)-t_(b)^(2)]`
`x=(g)/(8)[t_(a)^(2)-t_(b)^(2)]`
Promotional Banner

Topper's Solved these Questions

  • MOTION IN STRAIGHT LINE

    AAKASH INSTITUTE|Exercise Try Yourself|40 Videos

  • MOTION IN STRAIGHT LINE

    AAKASH INSTITUTE|Exercise Assignment (SECTION - A)|50 Videos

  • MOTION IN A STRAIGHT LINE

    AAKASH INSTITUTE|Exercise ASSIGNMENT (SECTION - D)|15 Videos

  • MOVING CHARGE AND MAGNESIUM

    AAKASH INSTITUTE|Exercise SECTION D|16 Videos

Similar Questions

Explore conceptually related problems

From a tower of height H, a particle is thrown vertically upwards with a speed u. The time taken by the particle, to hit the ground, is n times that taken by it to reach the highest point of its path. The relation between H, u and n is

A particle is thrown vertically upwards from the surface of the earth. Let T_(P) be the time taken by the particle to travel from a point P above the earth to its highest point and back to the point P. Similarly, let T_(Q) be the time taken by the particle to travel from another point Q above the earth to its highest point and back to the same in terms of T_(P), T_(Q) and H, is :-

In the following displacement (x) vs time (t) graph, at which among the point P,Q and R is the object speed increasing ?

Normals drawn to the hyperbola xy=2 at the point P(t_1) meets the hyperbola again at Q(t_2) , then minimum distance between the point P and Q is

The reation between the time t and position x for a particle moving on x-axis is given by t=px^(2)+qx , where p and q are constants. The relation between velocity v and acceleration a is as

A car starts from a point P at time t = 0 seconds and stops at point Q. The distance x, in metres, covered by it, in t seconds is given by x=t^2(2-t/3) Find the time taken by it to reach Q and also find distance between P and Q.

In following displacement (x) vs time (t) graph at which among the P,Q and R is the object's speed increasing ?

Point of intersection of normal at P(t1) and Q(t2)