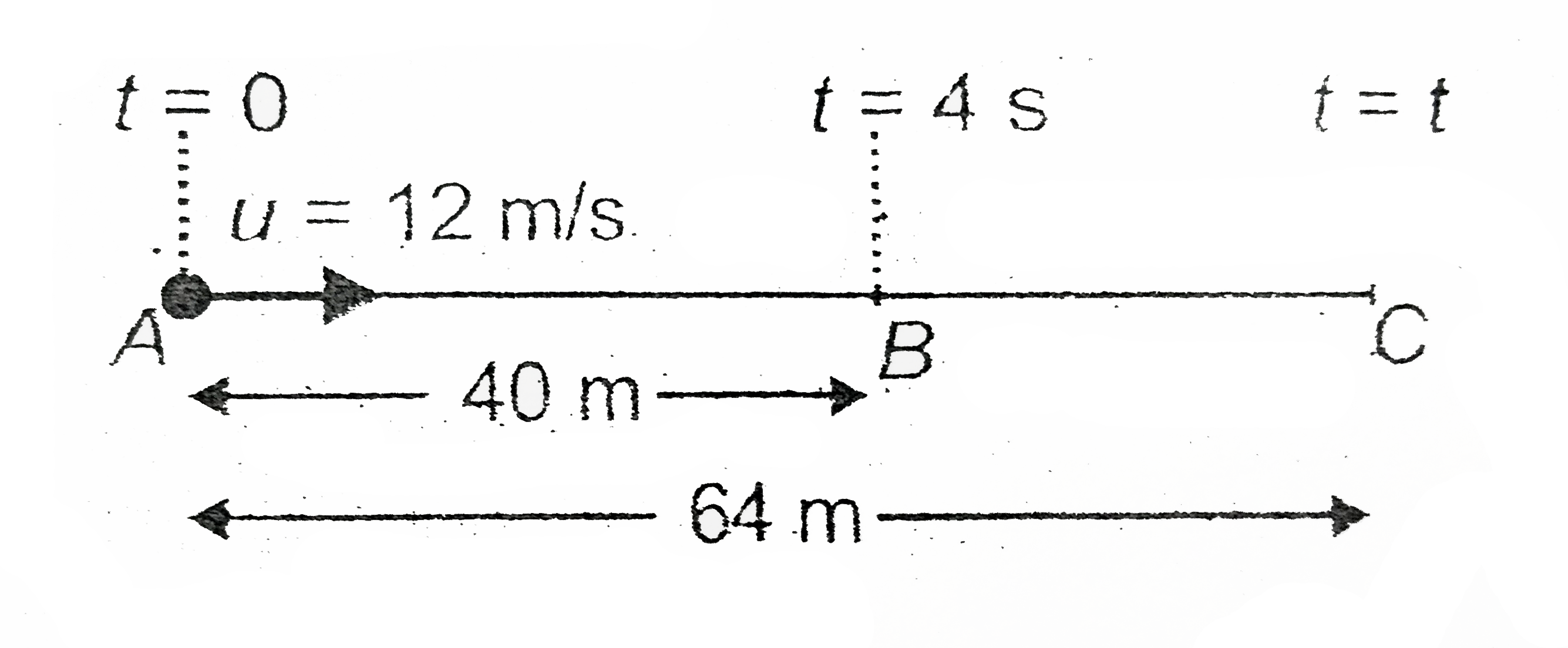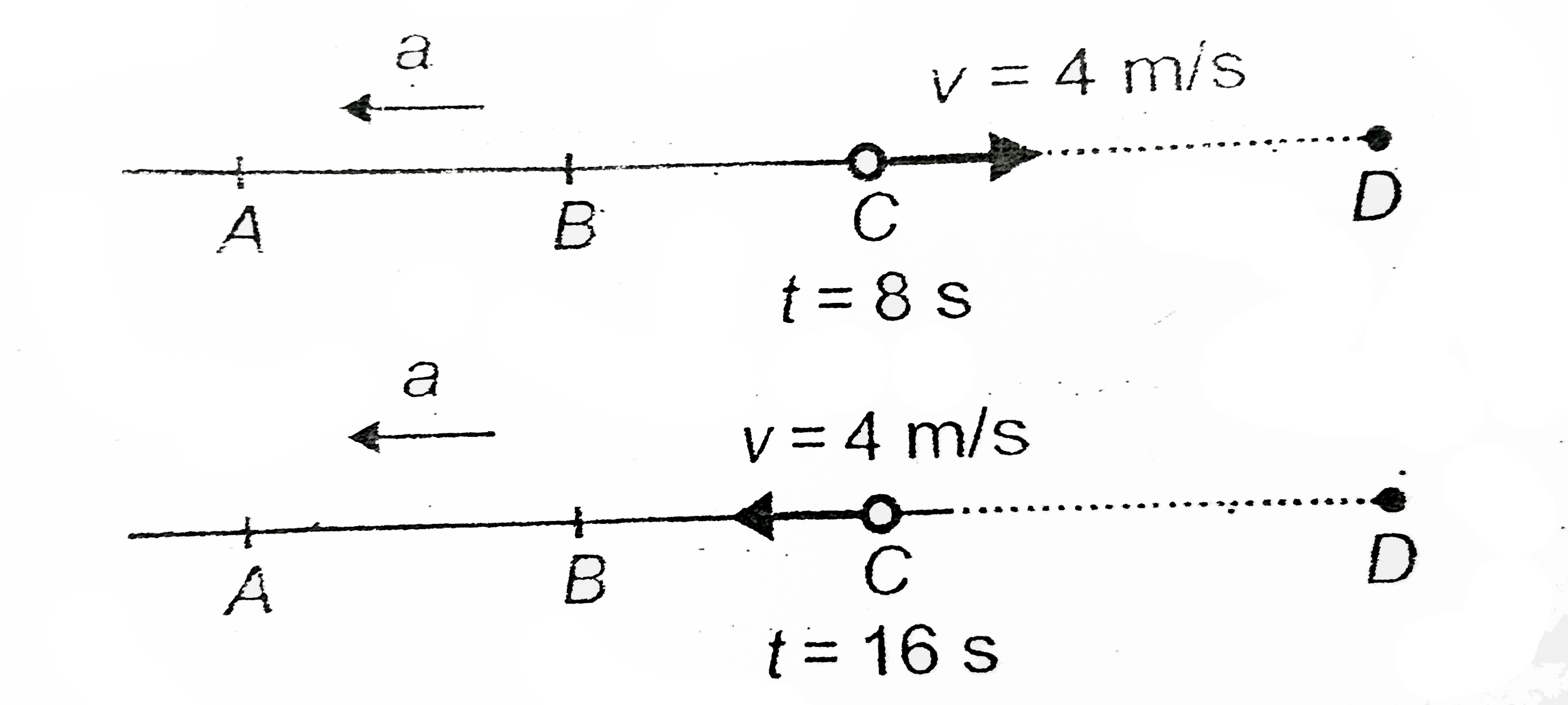Home
Class 12
PHYSICS
A particle, moving with uniform accelera...

A particle, moving with uniform acceleration along a straight line ABC, crosses point A at t = 0 with a velocity 12 m/s. B is 40 m from A and C is 64 m from A. The particle passes B at t = 4 s.
(a) At what time, will the particle be C?
(b) What is its velocity at C?

Text Solution

Verified by Experts

(a) Let the acceleration of particle be a.
For motion between A and B
`u=12m//s, s=40 m, t=4s`
Using `s=ut+(1)/(2)at^(2)`, we get

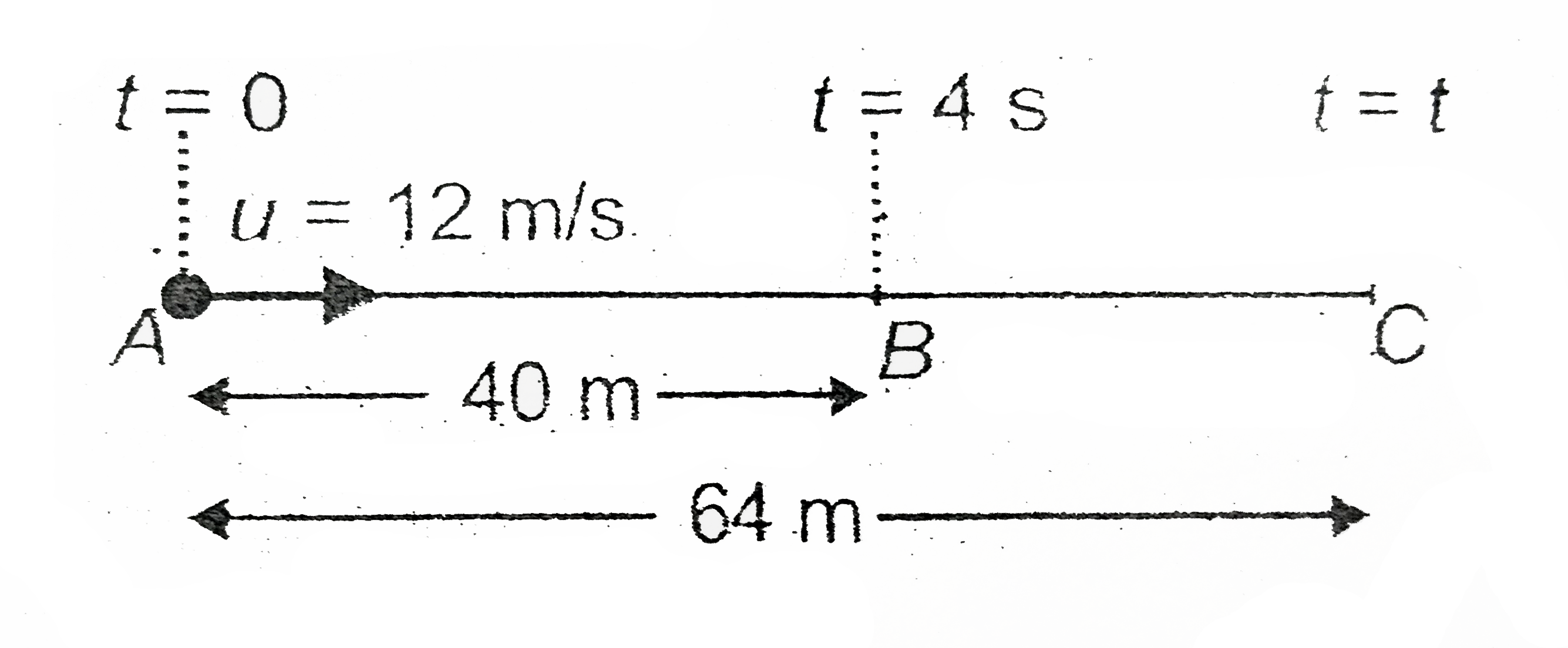
`40=12(4)+(1)/(2)a(4)^(2)`
`rArr a=-1m//s^(2)`
For motion between A and C
Let particle reaches C at time t.
`u=12m//s, s=64 m`
`rArr 64=12t+(1)/(2)(-1)t^(2)`
`rArr t^(2)-24t+128=0`
`rArr (t-8)(t-16)=0`
`rArr t=8s and t=16s` (why double answer?)
`rArr` The particle will be at C twice, at t = 8 s and t = 16 s.
(b) Velocityk of particle at C :
At t = 8 s, velocity at C is given by `v=12+(-1)xx8=4m//s`
and at t = 16 s velocity of particle is given by `v=12+(-1)xx16-4m//s`

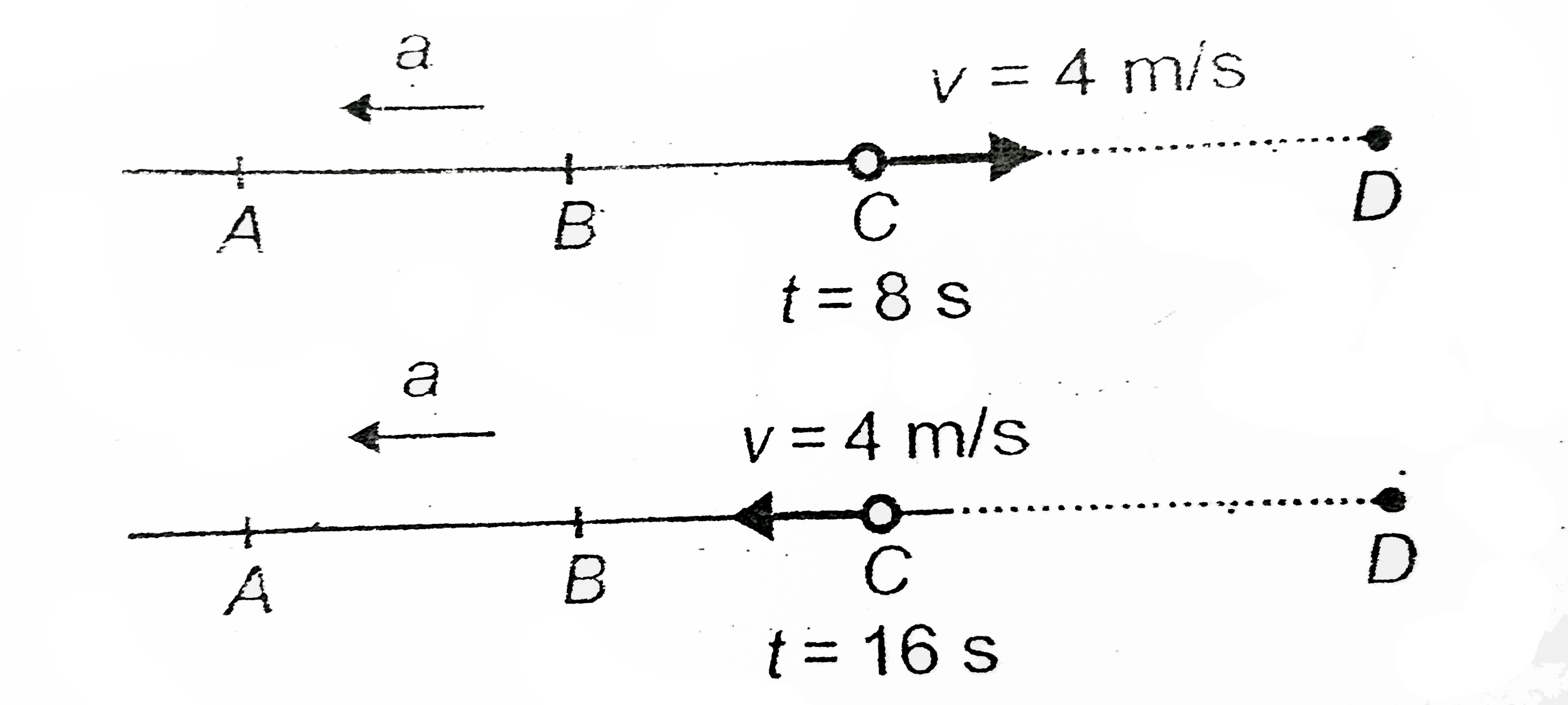
As the acceleration of particle is opposite to velocity, its speed decreases as it moves along ABC. At a point beyond C (say at D), the particle will come to rest momentarily, and then it will move backward with increasing speed and crosses point C again. This explains the double answer for time in part (a).
Promotional Banner

Topper's Solved these Questions

  • MOTION IN STRAIGHT LINE

    AAKASH INSTITUTE|Exercise Try Yourself|40 Videos

  • MOTION IN STRAIGHT LINE

    AAKASH INSTITUTE|Exercise Assignment (SECTION - A)|50 Videos

  • MOTION IN A STRAIGHT LINE

    AAKASH INSTITUTE|Exercise ASSIGNMENT (SECTION - D)|15 Videos

  • MOVING CHARGE AND MAGNESIUM

    AAKASH INSTITUTE|Exercise SECTION D|16 Videos

Similar Questions

Explore conceptually related problems

A particle moving with uniform acceleration along a straight line ABC rosses point A at t=0 with a velocity 12 m s^(-1) . is 40 m away from A and C is 64 m away from A . The particle passes B at t=4 s . a. After what time will the particle be at C ? b. What is its velocity at C ? c. What does the particle reach A again? d. Locate the point where the particle reverses its direction of motion. e. Find the distance covered by the particle in the first 15 s .

A particle is moving with uniform acceleration along a straight line ABC. Its velocity at A and B are 6 m/s and 9 m/s respectively if AB:BC=5:16 then its velocity at C is

A particle is moving with uniform acceleration along a straight line ABC, where AB= BC. The average velocity of the particle from A to B is 10 m/s and from B to C is 15 m/s. The average velocity for the whole journey from A to C in m/s is

A particle is moving with uniform acceleration along a straight line "ABC" .Its velocity at A and B are 6m/s" and "9m/s respectively. If AB:BC=5:16" then its velocity at C is

A particle moving with uniform acceleration passes the point x=2m with velocity 20 m//s at the instant t=0 . Some time later it is observed at the point x=32 m moving with velocity 10 m//s . (a) What is its acceleration? (b) Find its position nd velocity at the instant t=8 s . (c) What is the distance traveled during the interval t=0 to 8s ?

A particle moves with uniform acceleration along a straight line AB . Its velocities at A and B are 2 m//s and 14 m//s respectively. M is the mid-point of AB . The particle takes t_1 seconds to go from A to M and t_2 seconds to go from M to B . Then t_2 : t_1 is.

A particle moving with uniform acceleration from A to B along a straight line has velcities v_(1) and v_(2) at A and B respectively. If C is the mid-point between A and B then determine the velocity of the particle at C . .

A particle is moving with uniform acceleration along a straight line. Its velocities at A & B are respectively 7 m//s & 17 m//s . M is mid point of AB. If t_(1) is the time taken to go from A to M and t_(2) the time taken to go from M to B, the ratio t_(1)/t_(2) is equal to :-

A particle is moving with uniform acceleration along a straight line. The average velocity of the particle from P to Q is 8ms^(–1) and that Q to S is 12ms^(–1) . If QS = PQ, then the average velocity from P to S is