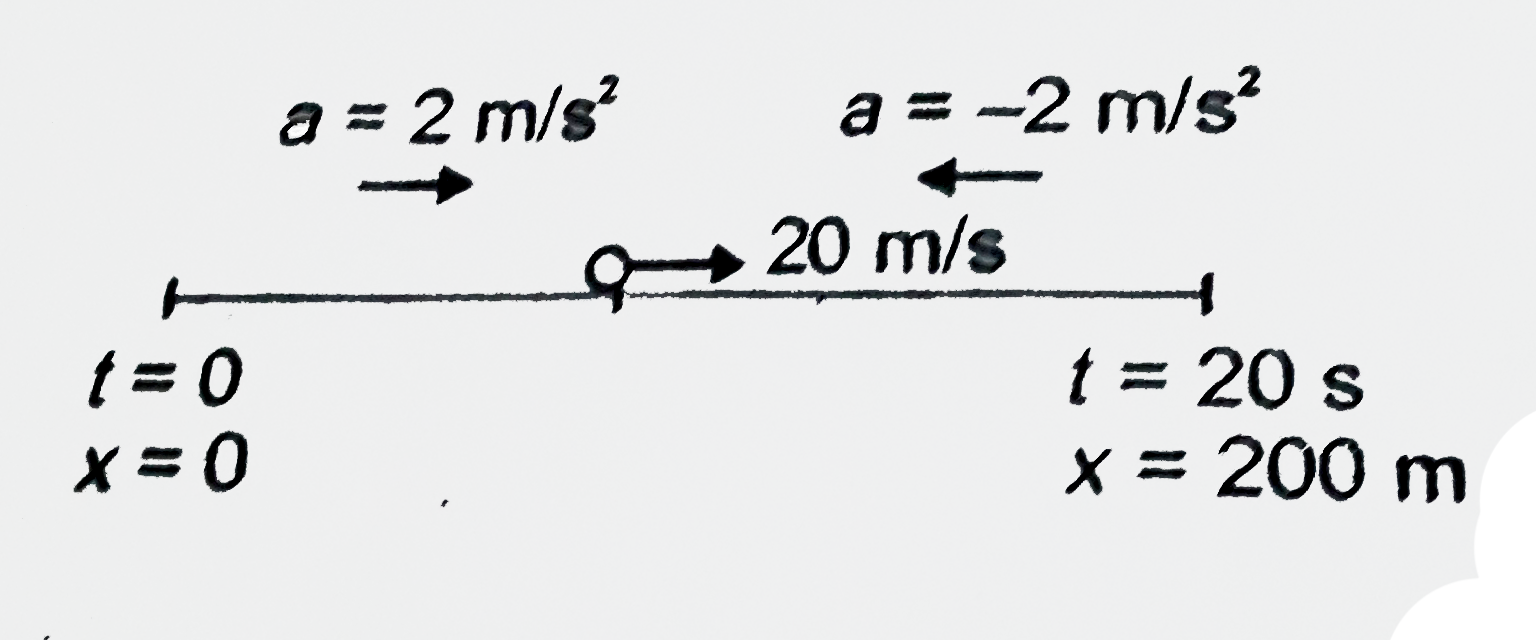Home
Class 12
PHYSICS
A particle starts from rest and accelera...

A particle starts from rest and accelerates constantly with `2m//s^(2)` for 10 s and then retards uniformly with same rate till it comes to rest. Draw the x-t, v-t and a-t graphs.

Text Solution

Verified by Experts

The velocity acquired by the particle at t = 10 s is 20 m/s `(v=u+at)`. It takes further 10 s to comes to rest under retardation of `2m//s^(2)`. Distance travelled in the interval 0 to 10 s is 100 m (use `s=ut+(1)/(2)at^(2)`) and the distance travelled in the interval 10 s to 20 s is also 100 m (use `v^(2)=u^(2)+2as`). Let the particle start from x = 0. The final position of particle is x = 200 m.

Fot t = 0 to t = 10 s, motion is uniformly accelerated with positive acceleration `a=+2m//s^(2)`. The x-t graph is a parabola opening upward. For t = 10 s to t = 20 s, motion is uniformly accelerated with negative acceleration `a=-2m//s^(2)`. The x-t graph is a parabola opening downward.
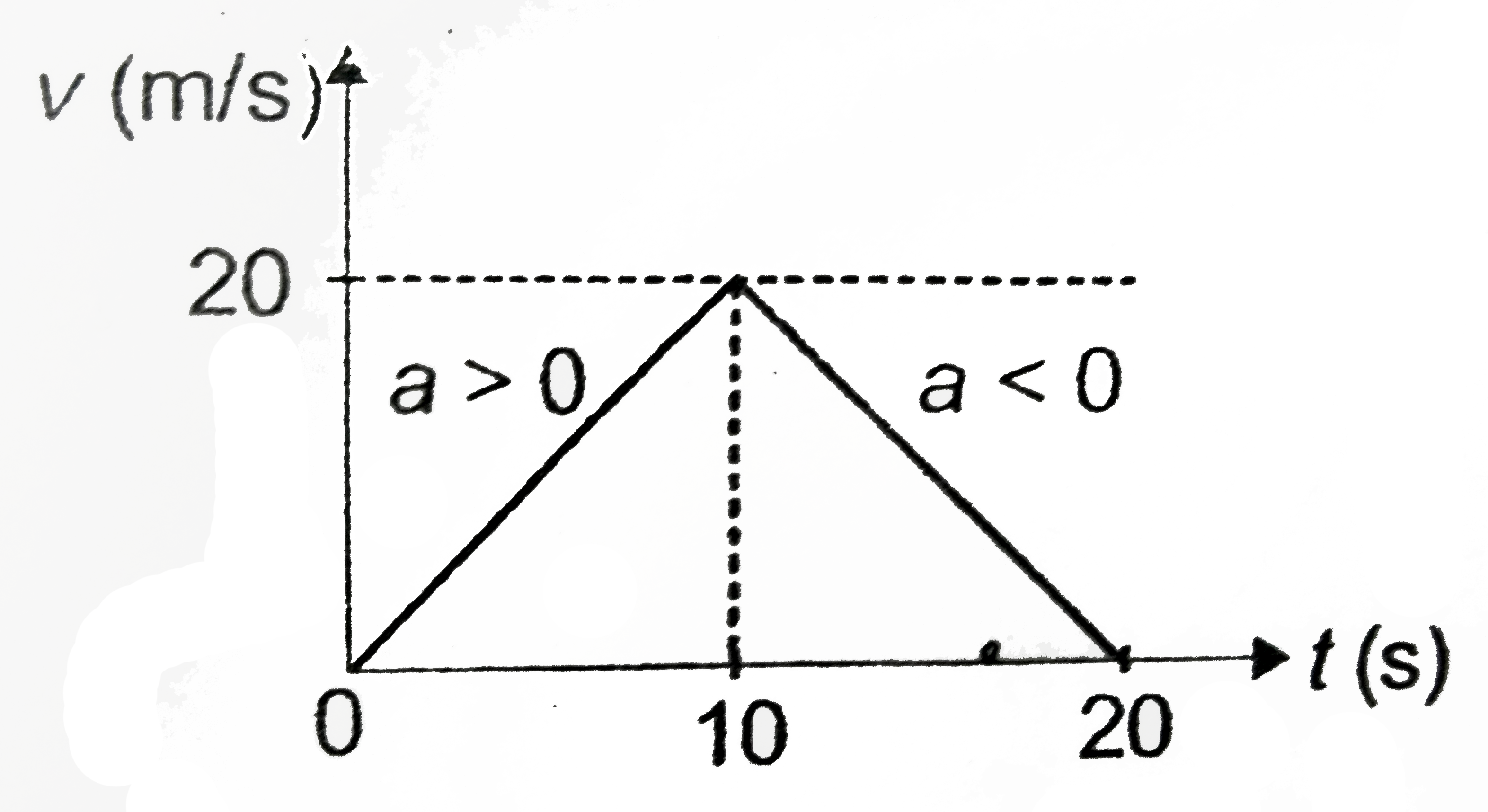
v-t graph

For t = 0 to t = 10 s, v-t graph is a straight line with positive slope and for t = 10 s to t = 20 s, the v-t graph is a straight line with negative slope. The intial and final velocities are zero.
a-t graph

For t = 0 to t = 10 s, a-t graph is a straight line parallel to time axis with `a=+2m//s^(2)` and for t = 10 s to t = 20 s. The a-t graph is straight line parallel to time axis with `a=-2m//s^(2)`.
Promotional Banner

Topper's Solved these Questions

  • MOTION IN STRAIGHT LINE

    AAKASH INSTITUTE|Exercise Try Yourself|40 Videos

  • MOTION IN STRAIGHT LINE

    AAKASH INSTITUTE|Exercise Assignment (SECTION - A)|50 Videos

  • MOTION IN A STRAIGHT LINE

    AAKASH INSTITUTE|Exercise ASSIGNMENT (SECTION - D)|15 Videos

  • MOVING CHARGE AND MAGNESIUM

    AAKASH INSTITUTE|Exercise SECTION D|16 Videos

Similar Questions

Explore conceptually related problems

A car accelerates from rest at the rate of 1m//s^(2) for 5 seconds and then retards at the same rate till it comes to rest. Draw the x-t, v-t and a-t graphs

A particle starting from rest has a constant acceleration of 4 m//s^2 for 4 s. It then retards uniformly for next 8 s and comes to rest. Find during the motion of particle (a) average acceleration (b) average speed and (c) average velocity.

A particle starts from rest accelerates at 2 m//s^2 for 10 s and then goes for constant speed for 30 s and then decelerates at 4 m//s^2 till it stops. What is the distance travelled by it.

A particle starts from rest, accelerates at 2(m)/(s^2) for 10 s and then goes for constant speed for 30 s and then decelerates at 4(m)/(s^2) . Till it stops. What is the distance travelled by it?

A particle starts from rest, accelerates uniformly for 3 seconds and then decelerates uniformly for 3 seconds and comes to rest. Which one of the following displacement (x)-time (t) graphs represents the motion of the particle?

A particle starts from rest and moves with an acceleration of a={2+|t-2|}m//s^(2) The velocity of the particle at t=4 sec is

An experimental car in fig (a) starts from rest and travels along a straight track such that it accelerates at a constant rate for 10 s and then decelerates at a constant rate draw the v-t and s-t graphs and determine the time t' needed to stop the car. how far has the car travelled.?

A body starts from rest & moves with constant acceleration a_1 for time t_1 then it retards uniformly with a_2 , in time t_2 and finally comes at rest. Find (t_1)/(t_2)

A car starts from rest and accelerates uniformly with 2 ms^(-2) . At t = 10 s, a stone is dropped out of the window 1 m high of the car. What are the (i) velocity, and (ii) acceleration of the stone at t = 10.1 s? (Neglect air resistance). Take g = 9.8ms^(-2) .

A particles starts from rest and has an acceleration of 2m//s^(2) for 10 sec. After that , it travels for 30 sec with constant speed and then undergoes a retardation of 4m//s^(2) and comes back to rest. The total distance covered by the particle is