Home
Class 12
PHYSICS
An object starts from rest from the poin...

An object starts from rest from the point A to rest at point B on the same straight line at a distance d. It moves over the first part of the distance with an acceleration `alpha m//s^(2)` and for the remainder the retardation `beta m//s^(2)`. Find the time taken to complete the journey.

Text Solution

Verified by Experts

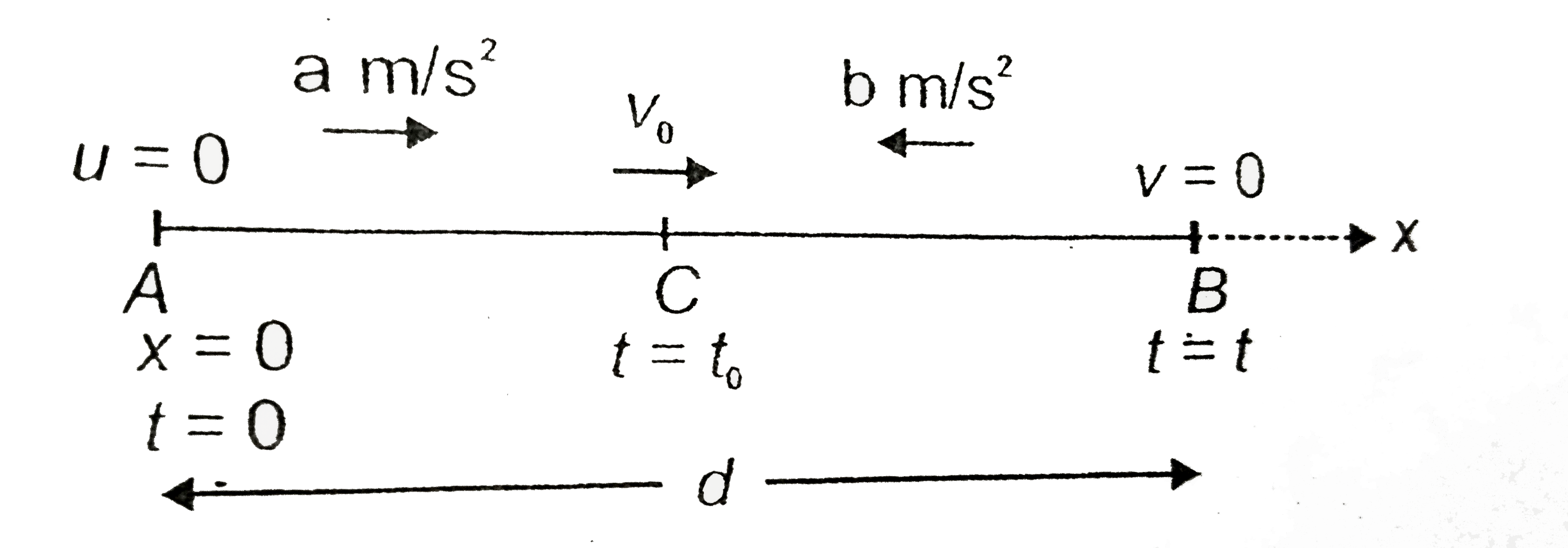
Method-I
Let C be the position where the speed of object is maximum `(v_(0))`. For A to C motion is uniformly accelerated and from C to B motion is retarded. We have
`d=AC+CB`
`rArr" "d=(v_(0)^(2))/(2alpha)+(v_(0)^(2))/(2beta)" "("use "v^(2)=u^(2)+2as" for AC and CB")`
`rArr" "v_(0)=sqrt((2alphabeta)/(alpha+beta)d)`
Total time taken

`t=t_(ArarrC)+t_(CrarrB)`
`rArr" "t=(v_(0))/(alpha)+(v_(0))/(beta)" (use v = u + at for AC and CB)"`
`rArr" "t=(v_(0)(alpha+beta))/(alpha beta)=sqrt((2alpha beta d)/((alpha+beta))).((alpha+beta)/(alpha beta))`
`rArr" "t=sqrt((2(alpha+beta))/(alpha beta)d)`
Method II Using the v-t graph
The v-t graph of the motion is shown. For the first part, the slope of v-t graph is equal to `alpha` and for the second part slope is equal to `-beta`. We have
Total distance travelled = Area under v-t graph
`rArr" "d=(1)/(2)v_(0)t" ...(i)"`
Also, `t=(v_(0))/(tan theta_(1))+(v_(0))/(tan theta_(2))`

`rArr" "t=v_(0)((1)/(alpha)+(1)/(alpha))`
`rArr" "v_(0)=(alpha beta t)/(alpha+beta)" ...(ii)"`
From (i) and (ii),
`t=sqrt((2(alpha+beta)d)/(alpha beta))`
Promotional Banner

Topper's Solved these Questions

  • MOTION IN STRAIGHT LINE

    AAKASH INSTITUTE|Exercise Try Yourself|40 Videos

  • MOTION IN STRAIGHT LINE

    AAKASH INSTITUTE|Exercise Assignment (SECTION - A)|50 Videos

  • MOTION IN A STRAIGHT LINE

    AAKASH INSTITUTE|Exercise ASSIGNMENT (SECTION - D)|15 Videos

  • MOVING CHARGE AND MAGNESIUM

    AAKASH INSTITUTE|Exercise SECTION D|16 Videos

Similar Questions

Explore conceptually related problems

The distance travelled by a particle starting from rest and moving with an acceleration 4/3m/s2 ,in the third-second is

A particle starts with a velocity of 2m//s and moves in a straight line with a retardation of 0.1m//s^(2) . The time that it takes to describe 15m is

A body travels a distance s in t seconds. It starts from rest and ends at rest . In the first part of the journey , it moves with constant acceleration f and in the second part with constant retardation r. the value of t is given by

A body starts from rest with an acceleration 2m//s^(2) till it attains the maximum velocity then retards to rest with 3m//s^(2) . If total time taken is 10 second, then maximum speed attained is

A particle starts moving along a line from zero initial velocity and comes to rest after moving distance d. During its motion it had a constant acceleration f over 2/3 of the distance, and covered the rest of the distance with constant retardation. The time taken to cover the distance is

A particle, initially at rest, starts moving in a straight line with an acceleration a=6t+4 m//s^(2) . The distance covered by it in 3 s is

A body starts from rest from the origin with an acceleration of 3 m//s(2) along the x-axis and 4 m//s^(2) along the y-axis. Its distance from the origin after 2 s will be

A body starts from rest from the origin with an acceleration of 6m//s^(2) along the x-axis and 8m//s^(2) along the y-axis. Its distance from the origin after 4 seconds will be

A car starts from rest and accelerates uniformly to a speed 50ms^(-1) over a distance of 250m . Find the acceleration and time taken by the car to cover this distance.