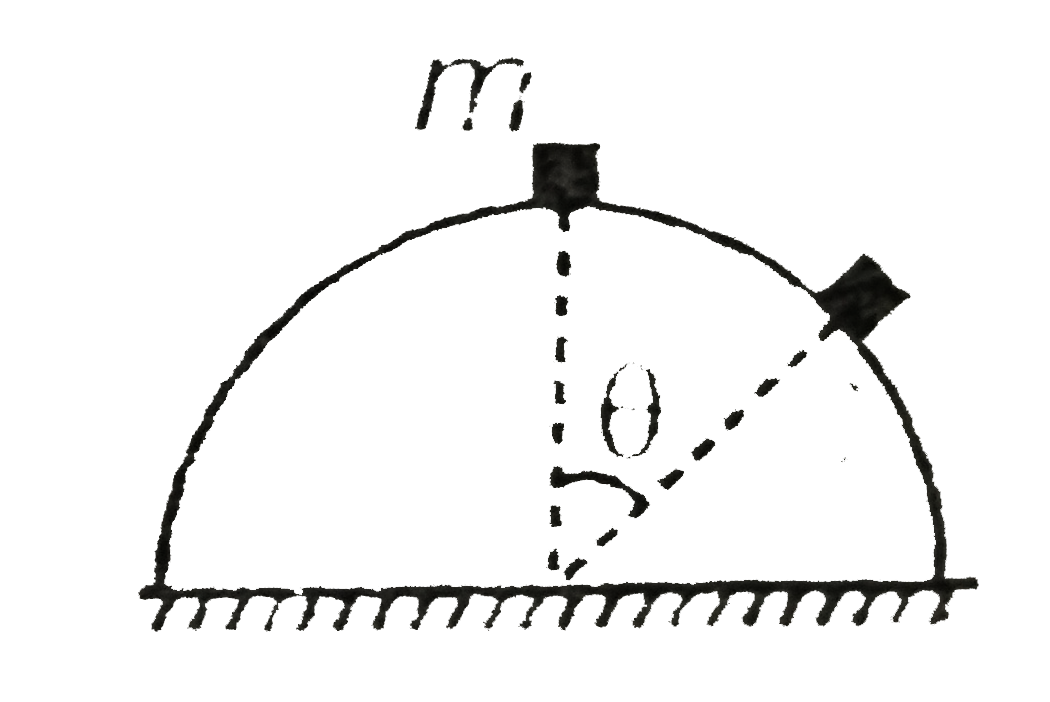Home
Class 12
PHYSICS
A particle of mass m is placed in equlib...

A particle of mass m is placed in equlibrium at the top of a fixed rough hemisphere of radius R. Now the particle leaves the contact with the surface of the hemisphere at angular position `theta` with the vertical wheere `cos theta""(3)/(5).` if the work done against frictiion is `(2mgR)/(10x),` find x.

Text Solution

Verified by Experts

The correct Answer is:
2
Promotional Banner

Topper's Solved these Questions

  • WORK, ENERGY AND POWER

    AAKASH INSTITUTE|Exercise SECTION-H (MULTIPLE TRUE FALSE TYPE QUESTIONS)|10 Videos

  • WORK, ENERGY AND POWER

    AAKASH INSTITUTE|Exercise SECTION-I (SUBJECTIVE TYPE QUESTIONS)|6 Videos

  • WORK, ENERGY AND POWER

    AAKASH INSTITUTE|Exercise SECTION-F (MATRIX-MATCH TYPE QUESTIONS)|4 Videos

  • WAVES

    AAKASH INSTITUTE|Exercise ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))|12 Videos

Similar Questions

Explore conceptually related problems

A particle is released from the top of the smooth hemisphere R as shown. the normal contact between the particle and the hemisphere in position theta is

A particle of mass m is released from the top of a smooth hemisphere of radius R with the horizontal speed mu . Calculate the angle with verticle where it loses contact with the hemisphere.

A particle of mass m initially at rest starts moving from point A on the surface of a fixed smooth hemisphere of radius r as shown. The particle looses its contact with hemisphere at point B.C is centre of the hemisphere. The equation relating theta and theta' is .

A block of mass as shown is released from rest from top of a fixed smooth hemisphere. Find angle made by this particle with vertical at the instant when it looses contact with hemisphere.

A particle rests on the top of a smooth hemisphere of radius r . It is imparted a horizontal velocity of sqrt(etagr) . Find the angle made by the radius vector joining the particle with the vertical at the instant the particle losses contact with the sphere.

A particle is released from the top of a smooth hemisphere.find the angle rotated by the radius through the particle, when it loses contract with the hemisphere. Also sketch variation of normal contact force with cos theta , where theta is an angle rotated by the radius through the particle.

A small particle is placed at the top point A of a fixed smooth hemisphere of radius R. Particle is given small displacement towards right and it starts slipping. Calculate velocity of the particle after hitting horizontal perfectly inelastic surface.

A particle of mass m is released on a fixed. Smooth sphere of radius R at a position, where the radius through the particle makes an angle of alpha with the verticle. What is the angle made by radius through the particle when the particle loses contact with sphere? (cos alpha=3//4)

A particle of mass m is released in a smooth hemispherical bowl from shown position A. Find work done by gravity as it reaches the lowest point B.