Home
Class 12
MATHS
Find the area enclosed between the parab...

Find the area enclosed between the parabola `4y=3x^2` and the straight line `3x-2y+12=0`

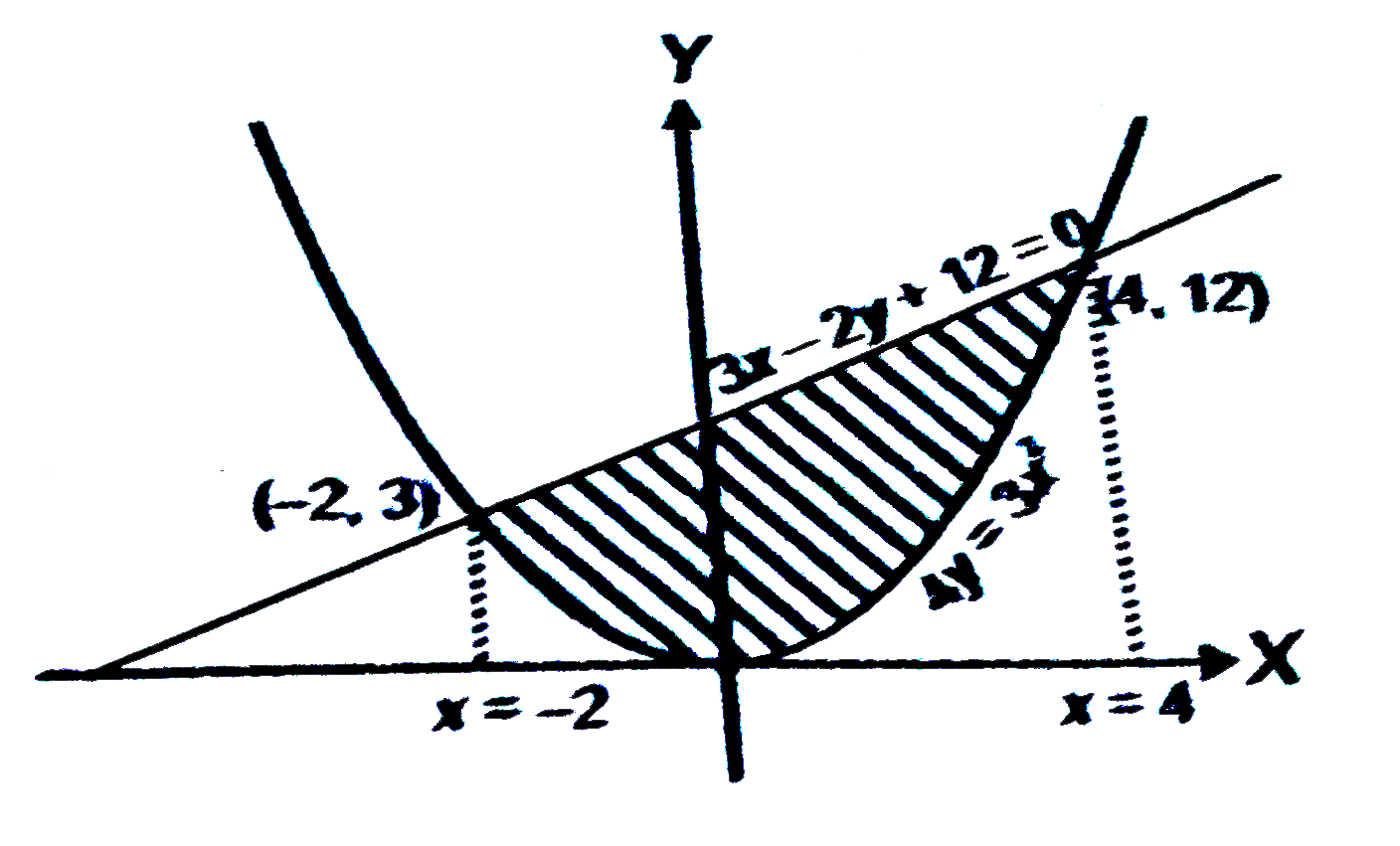
Text Solution

Verified by Experts

Solving ` y = (3x^(2))/(4)` and `3x - 2y + 12= 0` , we get `x = -2 , 4`
Area = `int_(-2)^(4) [((3x + 12)/(2)) - (3x^(2))/(4)]` dx
`= (3)/(4) [x^(2)]_(-2)^(4) + 6[x]_(-2)^(4) - (3)/(4) [(x^(3))/(3)]_(-2)^(4)`
=27 sq. units
Promotional Banner

Topper's Solved these Questions

  • APPLICATION OF INTEGRALS

    AAKASH INSTITUTE|Exercise Try Yourself|4 Videos

  • APPLICATION OF INTEGRALS

    AAKASH INSTITUTE|Exercise Assignment Section - A Competition Level Questions|24 Videos

  • APPLICATION OF DERIVATIVES

    AAKASH INSTITUTE|Exercise Assignment SECTION-J (Aakash Challengers Questions )|8 Videos

  • BINOMIAL THEOREM

    AAKASH INSTITUTE|Exercise Assignment (section-J) Objective type question (Aakash Challengers Questions)|4 Videos

Similar Questions

Explore conceptually related problems

Find the area enclosed by the parabola y = 2 - x^(2) and the straight line x + y = 0

Find the area enclosed between the parabola y^(2)=4ax and the line y=mx

Find the area enclosed between the circle x^2+y^2=25 and the straight line x+y=5 .

Find the area bounded by the parabola y=x^(2)+1 and the straight line x+y=3

Find the area bounded by the parabola y=2-x^(2) and the straight line y+x=0

Find the area enclosed by the parabola 4y=3x^(2) and the line 2y=3x+12

Find the area enclosed by the curve y=-x^(2) and the straight line x+y+2=0 .

Find the area bounded by the parabola y^2=4x and the straight line x+y=3 .

The area enclosed by the parabola y=3(1-x^(2)) and the x-axis is