Similar Questions
Explore conceptually related problems
Recommended Questions
- A uniform solid sphere of radius r is rolling on a smooth horizontal s...
Text Solution
|
- A sphere rolling on a horizontal rough surface Collides elastically wi...
Text Solution
|
- A uniform solid sphere of radius r is rolling on a smooth horizontal s...
Text Solution
|
- A solid sphere with a velocity (of centre of mass) v and angular veloc...
Text Solution
|
- A sphere is performing pure rolling on a rough horizontal surface with...
Text Solution
|
- A uniform solid sphere of radius r is rolling on a smooth horizontal s...
Text Solution
|
- A sphere of radius R and mass M collides elastically with a cubical bl...
Text Solution
|
- A solid sphere is set into motion on a rough horizontal surface with a...
Text Solution
|
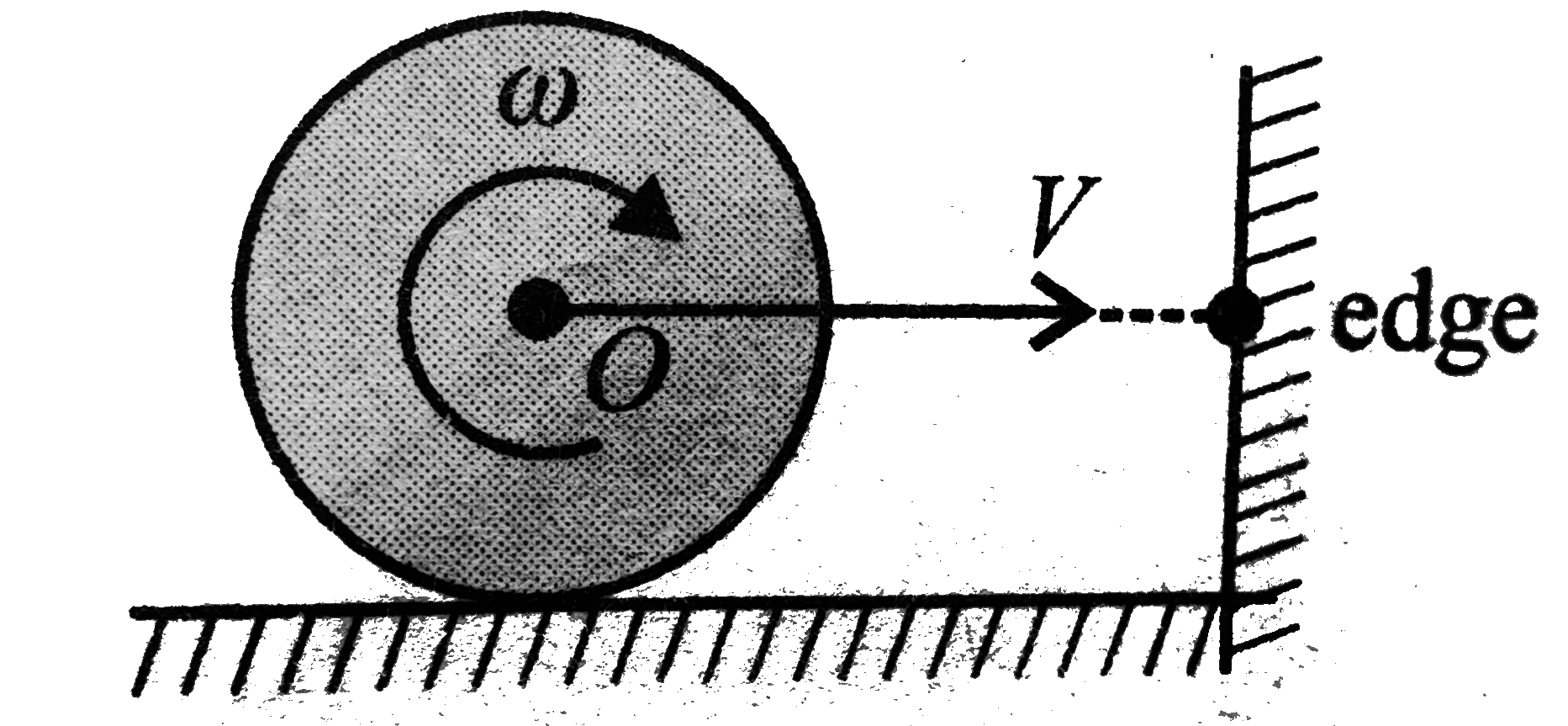
- a sphere rolling with velocity V collides a vertical wall. The frictio...
Text Solution
|