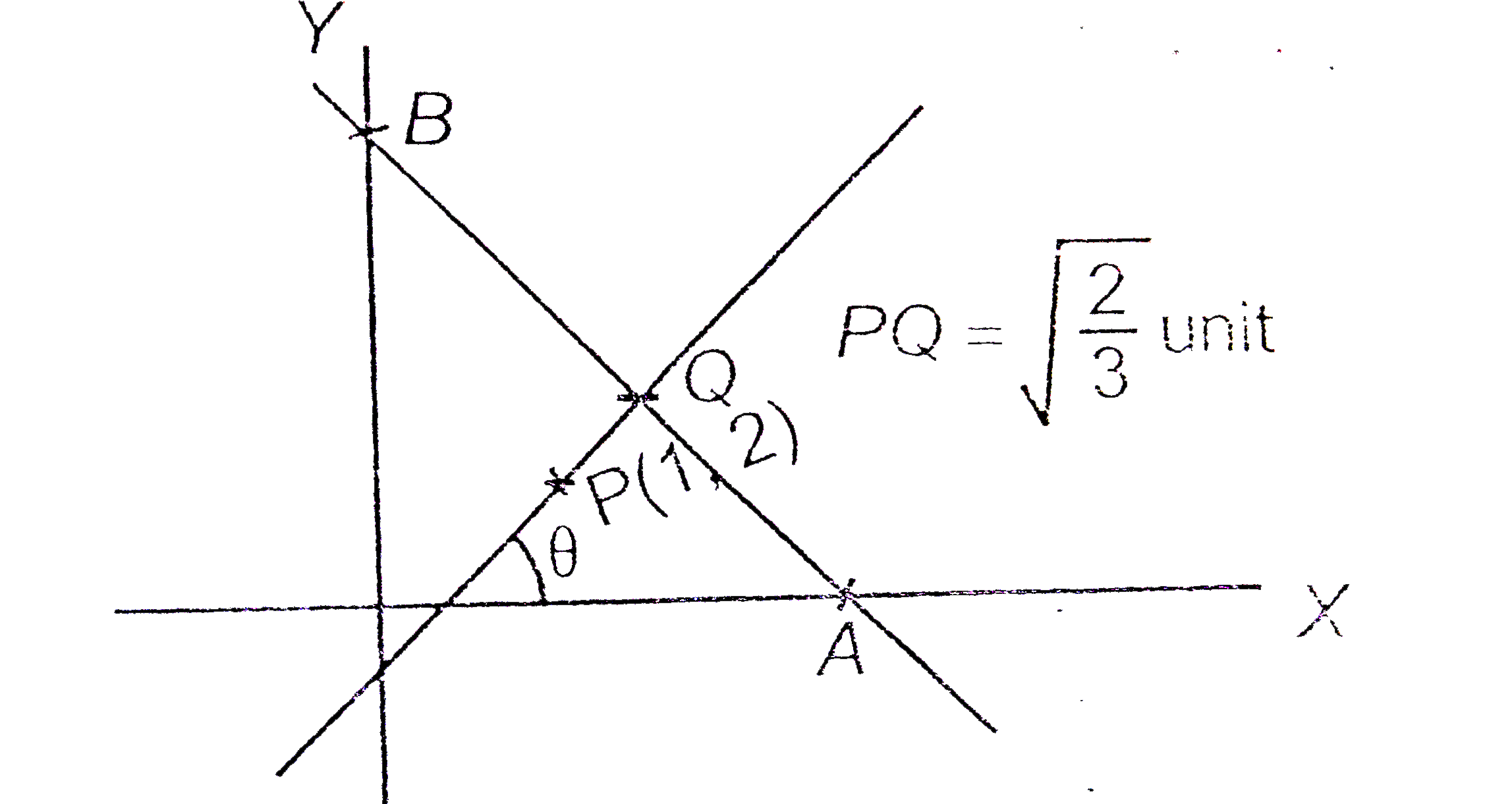
Text Solution
Verified by Experts
Topper's Solved these Questions
STRAIGHT LINES
AAKASH INSTITUTE|Exercise TRY YOURSELF|23 VideosSTRAIGHT LINES
AAKASH INSTITUTE|Exercise ASSIGNMENT (SECTION A) (OBJECTIVE TYPE QUESTIONS) (ONLY ONE ANSWER)|50 VideosSTATISTICS
AAKASH INSTITUTE|Exercise Section-C Assertion-Reason|15 VideosTHREE DIMENSIONAL GEOMETRY
AAKASH INSTITUTE|Exercise ASSIGNMENT SECTION - J|10 Videos
Similar Questions
Explore conceptually related problems
AAKASH INSTITUTE-STRAIGHT LINES-SECTION-J (AAKASH CHALLENGERS QUESTIONS)
- (i) Find the direction in which a straight line must be drawn torough ...
Text Solution
|
- The lines xy=0and x+y=17 from a triangle in the x-y plane. The total n...
Text Solution
|
- A line passes through A(1, 1) and B(100, 1000). The number of points w...
Text Solution
|
- In a A B C ,A-=(alpha,beta),B-=(1,2),C-=(2,3), point A lies on the li...
Text Solution
|
- Let P (sin theta, cos theta) (0 le theta le 2pi) be a point and let OA...
Text Solution
|
- The equation of two equal sides AB and AC of an isosceies triangle ABC...
Text Solution
|