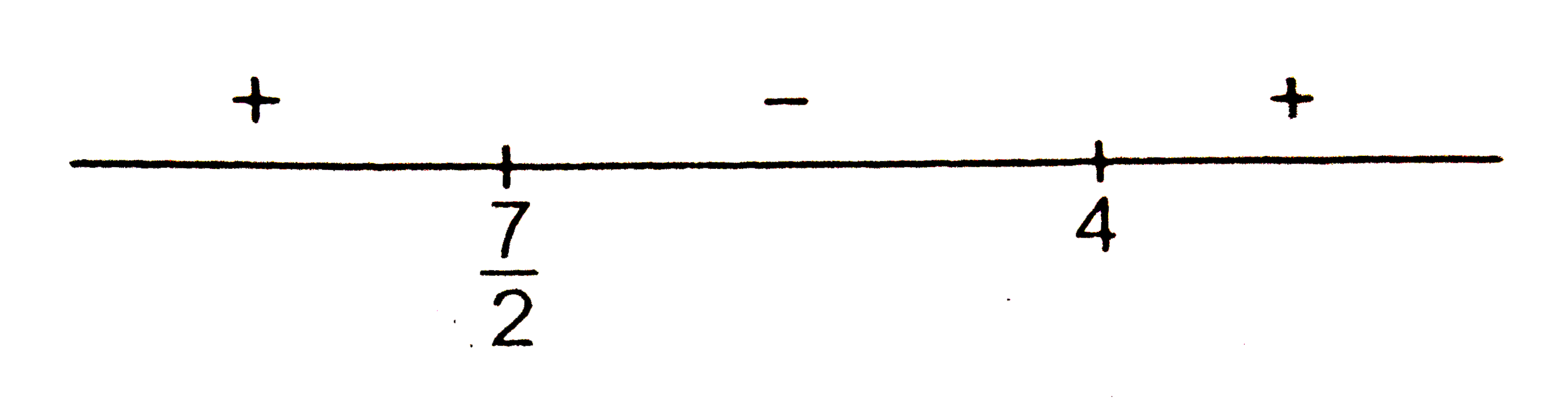
Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
AAKASH INSTITUTE-APPLICATION OF DERIVATIVES-Assignment SECTION-J (Aakash Challengers Questions )
- Find the intervals in which f(x)=4x^(3)-45x^(2)+168x-16 is (i) Stri...
Text Solution
|
- The area of the triangle formed by the tangent to the curve y=(8)/(4+...
Text Solution
|
- Any tangent at a point p(x,y) to the ellipse (x^(2))/(8)+(y^(2))/(18)...
Text Solution
|
- If the tangent at P(1,1) on the curve y^(2)=x(2-x)^(2) meets the curv...
Text Solution
|
- The curve y=ax^(3)+bx^(2)+cx is inclined at 45^(@) to x-axis at (0,0...
Text Solution
|
- Let f(x)=2x^(3)+ax^(2)+bx-3cos^(2)x is an increasing function for all...
Text Solution
|
- Let g(x)=2f(x/2)+f(2-x) and f''(x) < 0 AA x in (0,2). If g(x) increa...
Text Solution
|
- If the equation 3x^2 + 4ax + b = 0 has at least one root in (0,1) such...
Text Solution
|
- The integral value of 'b' for which the function f(x) = (b^2 - 3b + 2)...
Text Solution
|