Similar Questions
Explore conceptually related problems
Recommended Questions
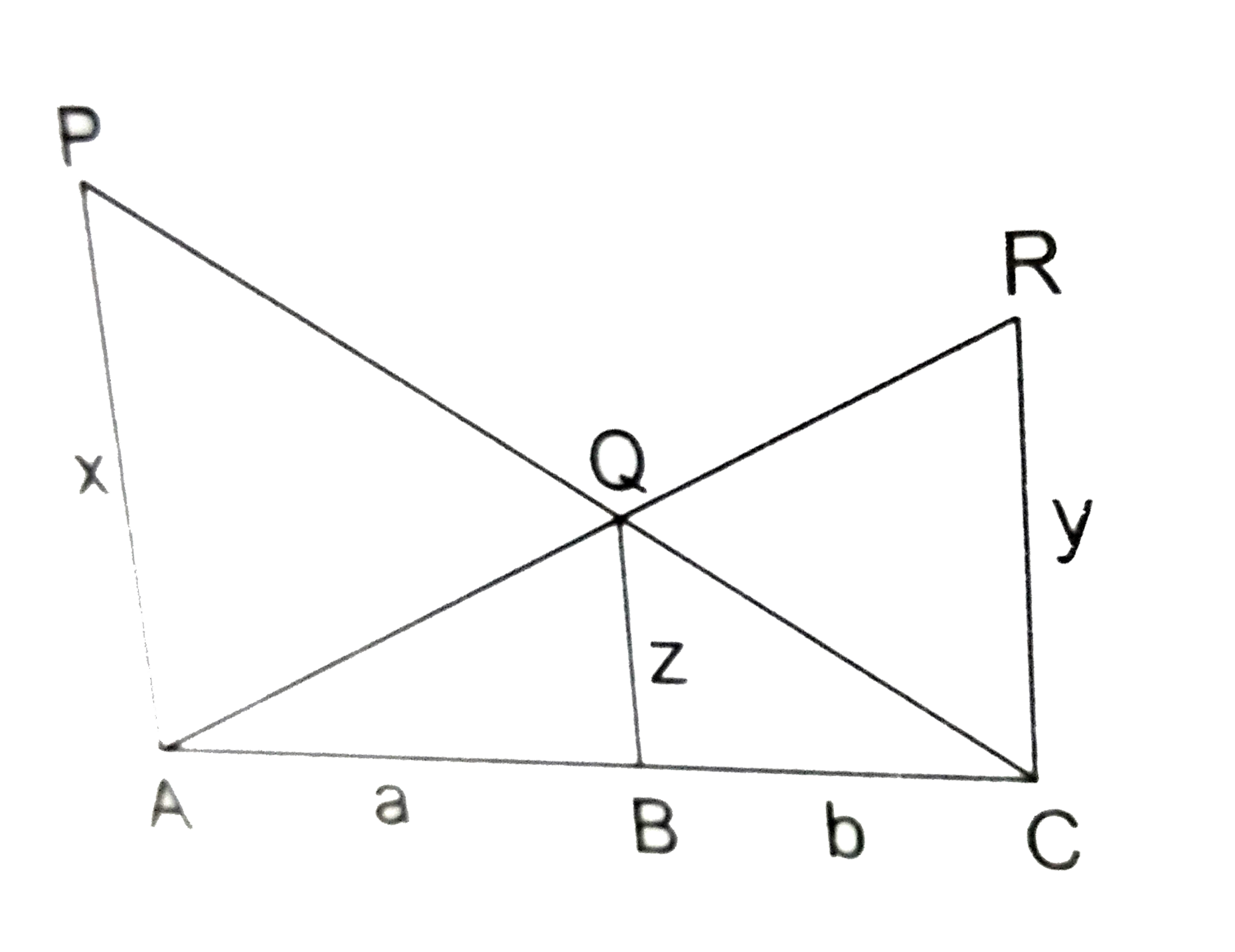
- In the given figure, PA, QB and RC each is perpendicular to AC such th...
Text Solution
|
- In Fig. 4.142, P A ,\ Q B and R C are each perpendicular to A C ...
Text Solution
|
- Determine the point of symmetry of a regular hexagon. <img src="htt...
Text Solution
|
- Dtermine the images of the following figure about the given line : ...
Text Solution
|
- Match the following Column A to Column B
Text Solution
|
- Match the following Column A to Column B
Text Solution
|
- Match the following Column A to Column B
Text Solution
|
- The inequation represented by the graph given below is : <img src="htt...
Text Solution
|
- The inequation that best describes the graph given below is <img src=...
Text Solution
|