Similar Questions
Explore conceptually related problems
Recommended Questions
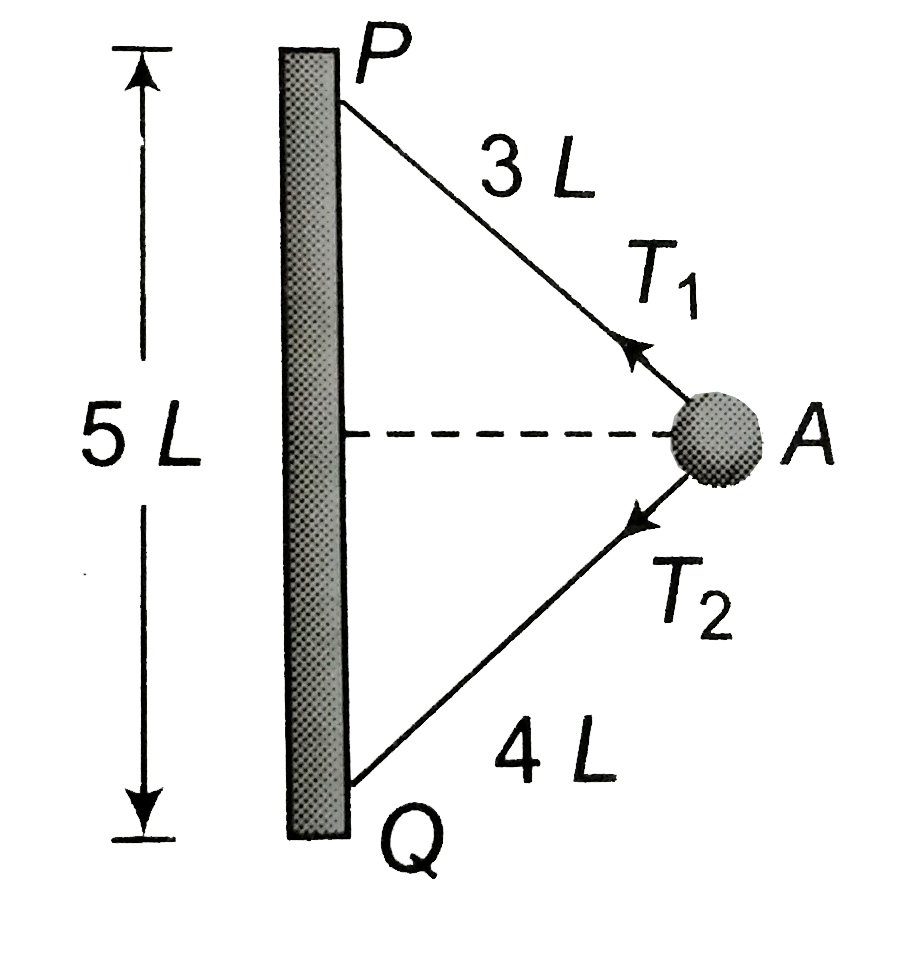
- A particle A of mass m is attached to a vertical axis by two stings PA...
Text Solution
|
- If the normals at points t1a n dt2 meet on the parabola, then t1t2=1 ...
Text Solution
|
- If the trace of matric A=[[sin^(2)theta,1,-13,-1,-3t(1),t(2),0]] is ze...
Text Solution
|
- A particle A of mass m is attached to a vertical axis by two stings PA...
Text Solution
|
- A particle P of mass m is attached to a vertical axis by two strings A...
Text Solution
|
- In fig tension in the string that connects the masses A and B is T(1) ...
Text Solution
|
- A particle P of mass m is attached to a vertical axis by two strings A...
Text Solution
|
- Two particles each of mass m are moving in horizontal circle with same...
Text Solution
|
- Determine the tension T(1) and T(2) in the strings
Text Solution
|