Similar Questions
Explore conceptually related problems
Recommended Questions
- Two graphs of the same projectile motion (in the xy-plane) projected f...
Text Solution
|
- Two graphs of the same projectile motion (in the x - y plane) projecte...
Text Solution
|
- Two graphs of the same projectile motion (in the xy-plane) projected f...
Text Solution
|
- Two graphs of the same projectile motion (in the xy-plane) projected f...
Text Solution
|
- Two graphs of the same projectile motion (in the xy-plane) projected f...
Text Solution
|
- A particle is projected from the horizontal x-z plane, in vertical x-y...
Text Solution
|
- A particle is projected in x-y plane with y-axis along vertical, the p...
Text Solution
|
- A particle is projected in xy plane with y-axis along vertical, the po...
Text Solution
|
- A particle is projected from origin in xy-plane and its equation ,of t...
Text Solution
|
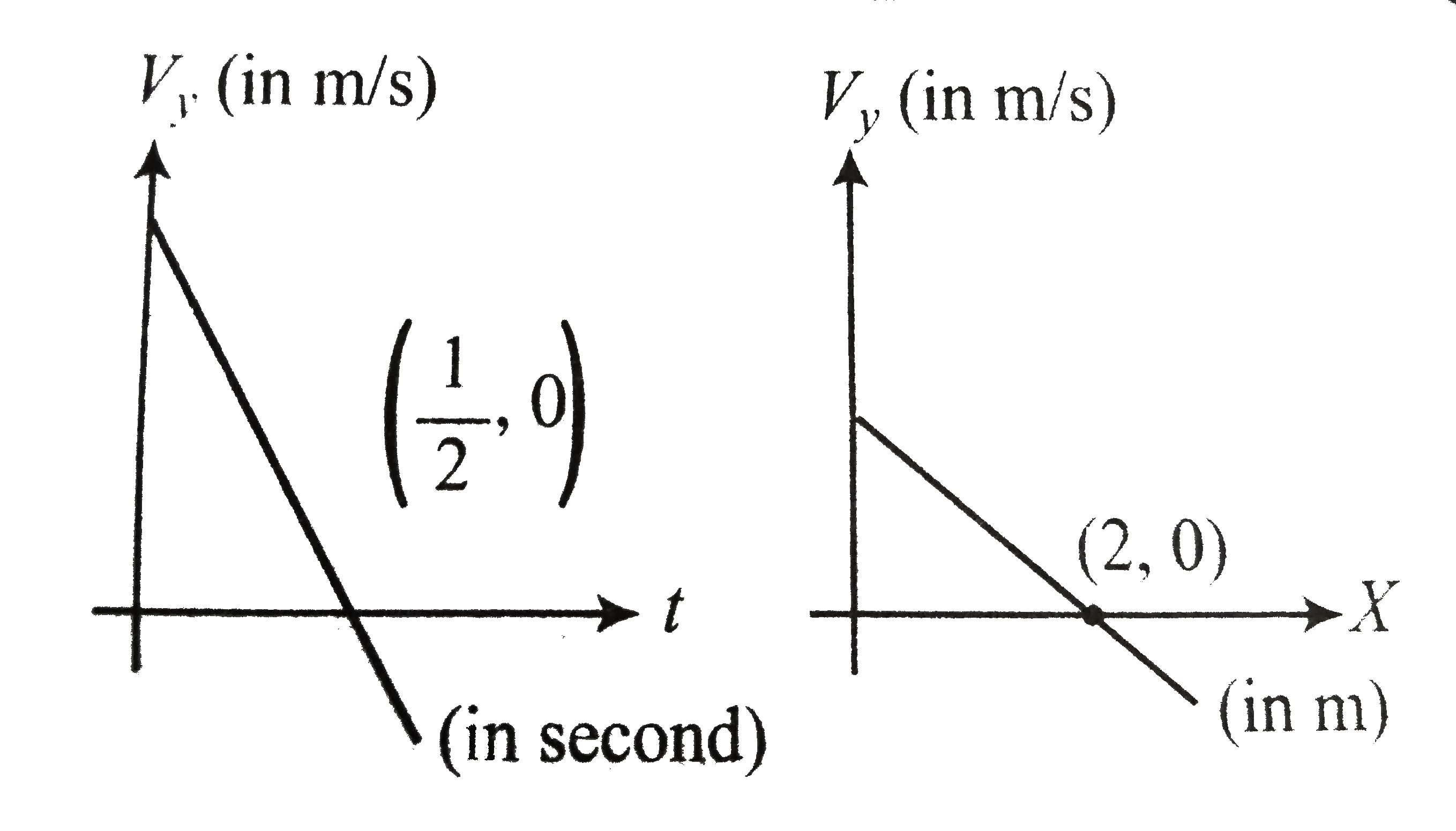 ,
,