Similar Questions
Explore conceptually related problems
Recommended Questions
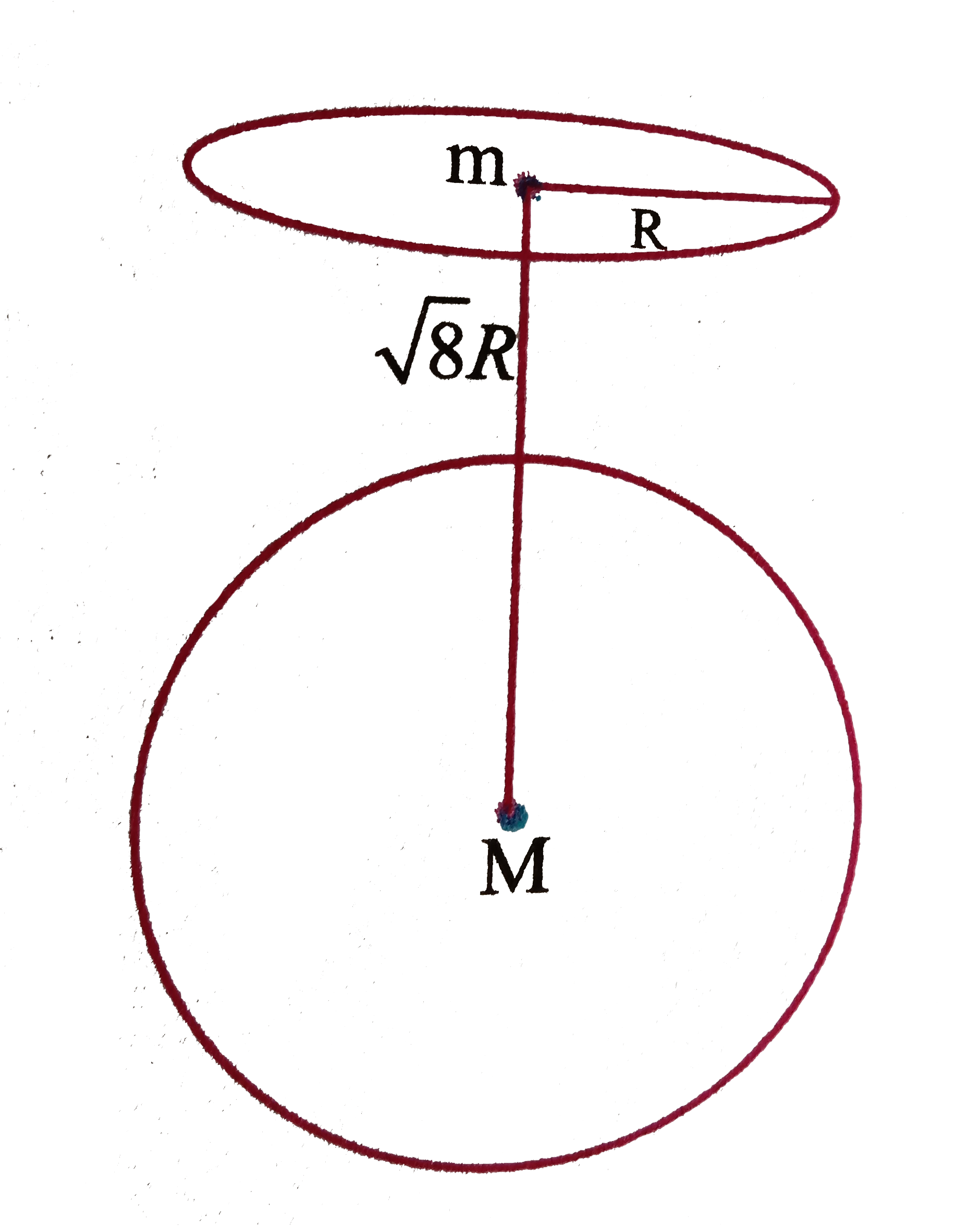
- The centres of a ring of mass m and a sphere of mass M of equal radius...
Text Solution
|
- A uniform ring of mass m is lying at a distance sqrt(3) a from the cen...
Text Solution
|
- The centres of a ring of mass m and a sphere of mass M of equal radius...
Text Solution
|
- An unchanged conducting sphere of radius R is placed near a uniformly ...
Text Solution
|
- Find the force of attraction on a particle of mass m placed at the cen...
Text Solution
|
- A uniform ring of mass M and radius R is placed directly above a unifo...
Text Solution
|
- A uiform ring of mass M and radius R is placed directly above a unifor...
Text Solution
|
- A uniform ring of mass m and radius 3a is kept above a sphere of mass ...
Text Solution
|
- A uniform ring of mass M and radius R is placed directly above a unifo...
Text Solution
|