Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
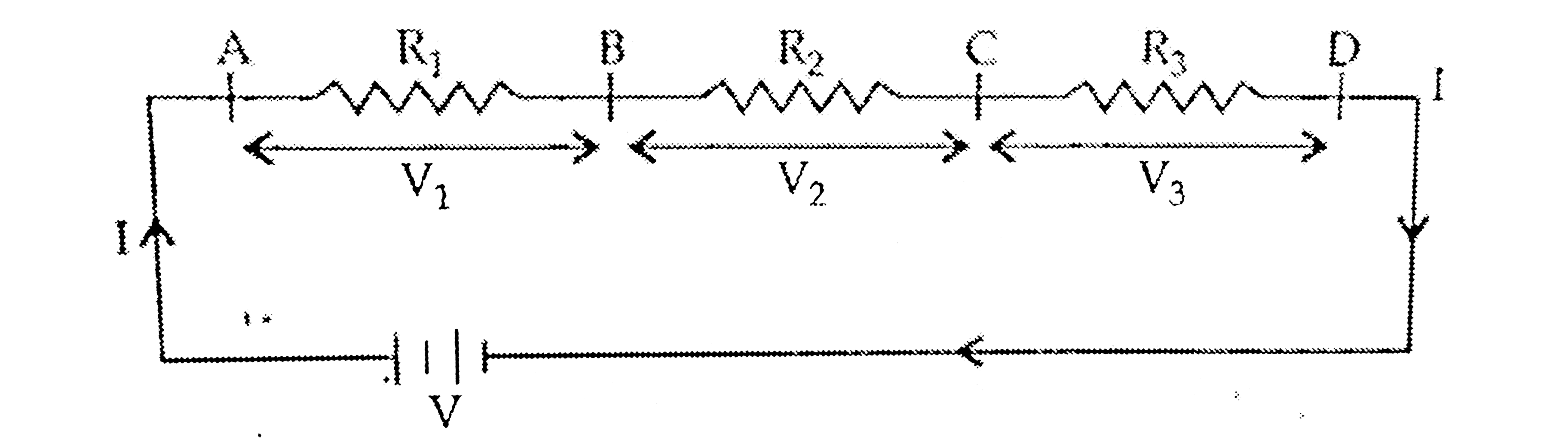
- For the series combination of three resistors establish the relation :...
Text Solution
|
- Two resistances R(1) = 100 +- 3 Omega and R(2) = 200 +- 4 Omega are co...
Text Solution
|
- Two resistor R(1) = (24 +- 0.5)Omega and R(2) = (8 +- 0.3)Omega are jo...
Text Solution
|
- Two resistor of resistance R(1)=(6+-0.09)Omega and R(2)=(3+-0.09)Omega...
Text Solution
|
- Two resistors of resistances R(1)=(300+-3) Omega and R(2)=(500+-4) Ome...
Text Solution
|
- For the series combination of three resistors establish the relation :...
Text Solution
|
- प्रतिरोधों का श्रेणी क्रम संयोजन क्या हैं? आपको R(1),R(2),R(3) Omega क...
Text Solution
|
- R(1)=(300pm 3)Omega एवं R(2)=(500pm 4)Omega की प्रतिरोधक क्षमता वाले द...
Text Solution
|
- R(1)=(100pm3)Omega तथा R(2)=(200pm4)Omega की प्रतिरोधक क्षमता वाले दो ...
Text Solution
|