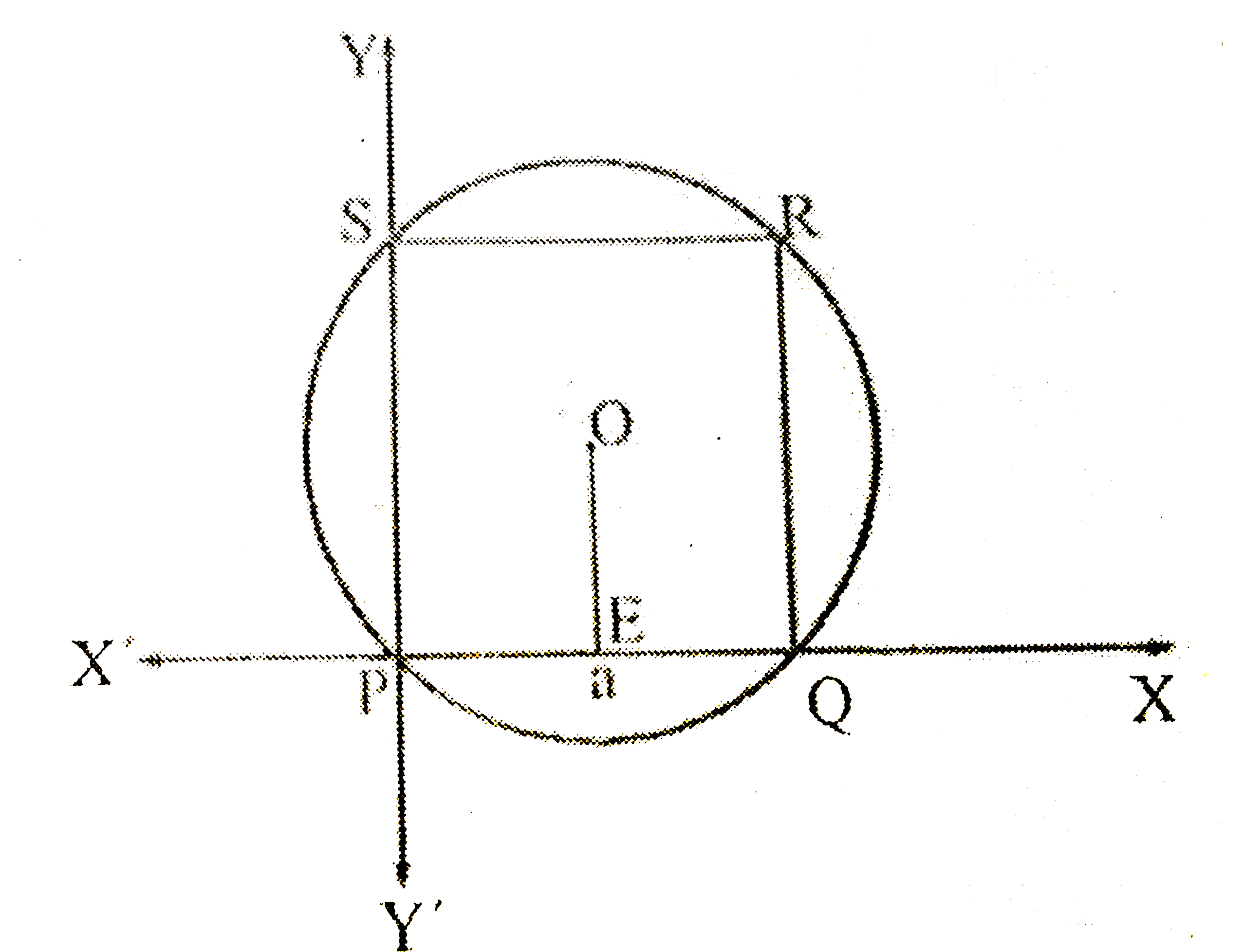माना PQ के अनुदिश x-अक्ष तथा PS के अनुदिश y-अक्ष है।
माना परिगत वृत्त का केन्द्र O है, जो वर्ग का भी केन्द्र होगा।
O से PQ पर लम्ब OE डाला, तब
`PE=OE=(1)/(2)a`
OP को मिलाया, तब समकोण `DeltaOEP` में,
`OP^(2)=PE^(2)+OE^(2)=((1)/(2)a)^(2)+((1)/(2)a)^(2)=(1)/(2)a^(2)`
`OP=(a)/(sqrt(2))`
वृत्त का केन्द्र `=((1)/(2)a,(1)/(2)a)`
तथा त्रिज्या `=(a)/(sqrt(2)).`
अत: परिगत वृत्त का अभीष्ट समीकरण निम्न है-
`(x-(1)/(2)a)^(2)+(y-(1)/(2)a)^(2)=((a)/(sqrt(2)))^(2)`
या `" "x^(2)+y^(2)-ax-ay=0" या "x^(2)+y^(2)=a(x+y).`