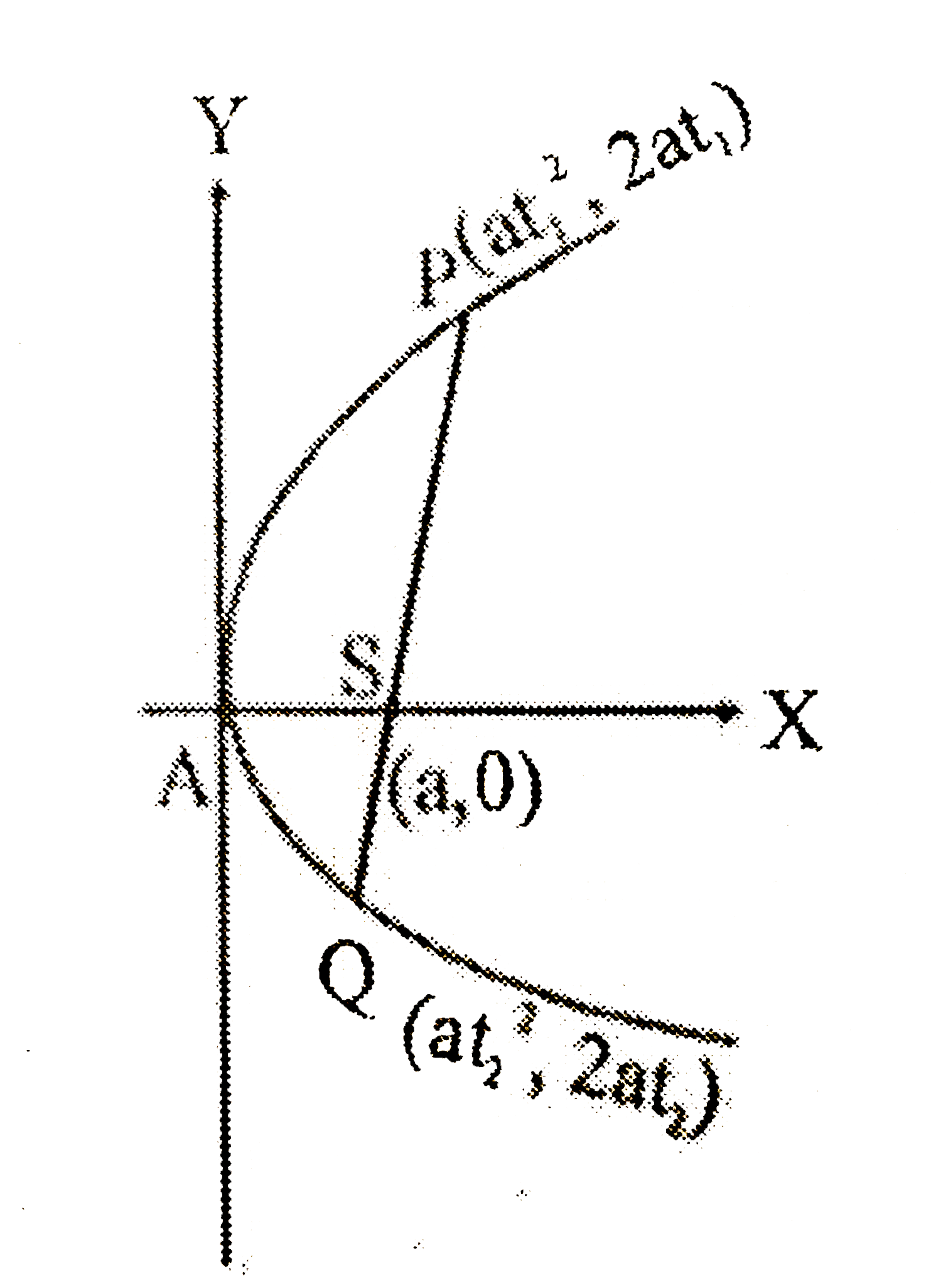
मान लीजिए परवलय की नाभीय जीवा PQ के एक सिरे का निर्देशांक `(at_(1)^(2),2at_(1))` तथा दूसरे सिरे का `(at_(2)^(2),2at_(2))` है।
अत: P और Q को मिलाने वाली रेखा का समीकरण
`y-2at_(1)=(2at_(2)-at_(1))/(at_(2)^(2)-at_(1)^(2))(x-at_(1)^(2))`
`implies" "y=-2at_(1)=(2)/(t_(2)+t_(1))(x-at_(1)^(2))`
परन्तु यह रेखा नाभि (a, 0) से होकर जाती है। अत:
`0-2at_(1)=(2)/(t_(2)+t_(1))(a-at_(1)^(2))`
या `" "-t_(1)(t_(2)+t_(1))=1-t_(1)^(2)`
या `" "-t_(1)t_(2)-t_(1)^(2)=1-t_(1)^(2)`
`implies" "t_(1)t_(2)=-1" या "t_(2)=-(1)/(t_(1))`
अत : नाभीय जीवा के दूसरे सिरे Q का निर्देशांक `((a)/(t_(1)^(2)),(2a)/(t_(1)))` है।
टिप्पणी : यदि नाभीय जीवा के एक सिरे का निर्देशांक `(at^(2),2at)` हो, तो दूसरे सिरे का निर्देशांक t के स्थान पर `-(1)/(t)` रखने पर प्राप्त होता है अर्थात यह `((a)/(t^(2)),(2a)/(t))` है।