मान लो A परवलय का शीर्ष और S नाभि है, तो
`OA=a,OS=a'`
`:." "As=OS-OA=a'`
`:.` शीर्ष A और नाभि S के निर्देशांक क्रमश: (a , 0) तथा (a', 0) हैं।
मान लो AS परवलय का अक्ष है, जिसका समीकरण y = 0 है।
SA को Z तक इतना बढ़ाओ की
`SA=AZ=a'-a`
`OZ=OA-ZA`
`=a-(a'-a)=2a-a'`
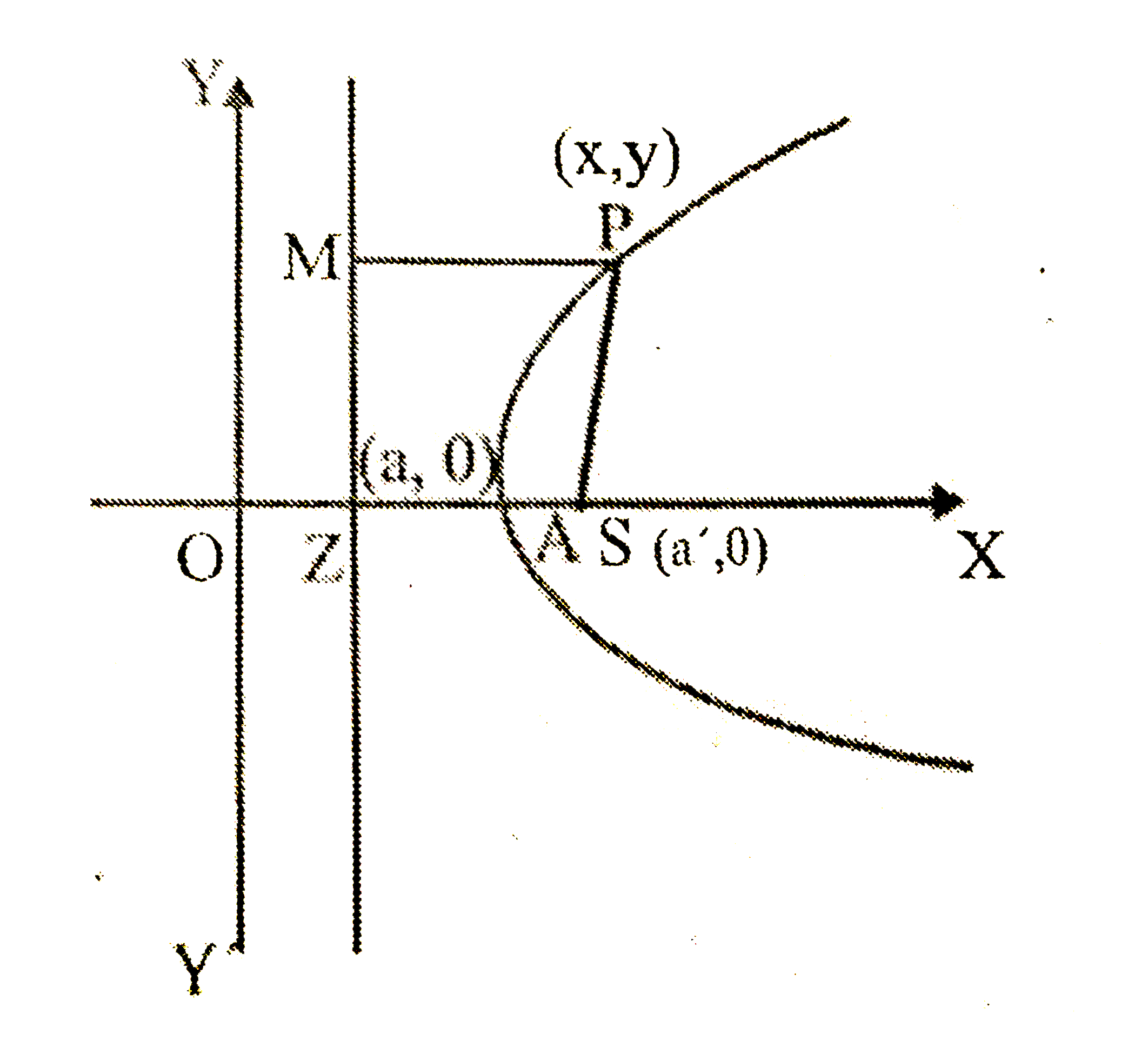
Z से होकर रेखा ZM खींचो, जो परवलय के अक्ष पट लम्ब है, तो ZM परवलय की नियता हुई, जिसका समीकरण `x=2a-a'`
या `" "x-2a+a'=0` है।
मान लो परवलय पर कोई बिन्दु P(x, y) है।
P से नियता पर लम्ब PM डालो और PS को मिलाओ,
तो परिभाषा से `" "SP=PM`
अर्थात `" "sqrt((x-a')^(2)+(y-0)^(2))=x-2a+a'`
या `" "(x-a)^(2)+y^(2)=(x-2a+a')^(2)`
या `" "y^(2)=(x-2a+a')^(2)-(x-a')^(2)`
या `" "y^(2)=4(a'-a)(x-a),` जो परवलय का अभीष्ट समीकरण है।